Spatial range of a morphogen gradient
Posted by stas, on 23 November 2011
Estimating the range of a morphogen gradient
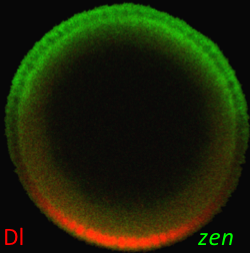 Morphogen gradient, defined as a concentration field of a chemical factor that acts as a dose-dependent regulator of cell differentiation, is an established concept in developmental biology. However, morphogen gradients in real systems are difficult to measure and mechanisms by which they control patterns of cell fates are heavily debated in the literature. In order to resolve some of the outstanding questions, it is essential to measure morphogen gradients in large numbers of embryos, at multiple developmental time points, and across multiple genetic backgrounds. We have developed a high throughput experimental approach that greatly facilitates these tasks for morphogens in the Drosophila embryo, a model system at the forefront of quantitative studies of development (Chung, Kim, et. al., Nature Methods 2011). In our recent Development paper, we used this technique to quantify the spatial range of the graded distribution of nuclear Dorsal, a transcription factor that subdivides the early fly embryo into presumptive muscle, skin, and nerve tissues (Kanodia et al, Development, 2011).
Morphogen gradient, defined as a concentration field of a chemical factor that acts as a dose-dependent regulator of cell differentiation, is an established concept in developmental biology. However, morphogen gradients in real systems are difficult to measure and mechanisms by which they control patterns of cell fates are heavily debated in the literature. In order to resolve some of the outstanding questions, it is essential to measure morphogen gradients in large numbers of embryos, at multiple developmental time points, and across multiple genetic backgrounds. We have developed a high throughput experimental approach that greatly facilitates these tasks for morphogens in the Drosophila embryo, a model system at the forefront of quantitative studies of development (Chung, Kim, et. al., Nature Methods 2011). In our recent Development paper, we used this technique to quantify the spatial range of the graded distribution of nuclear Dorsal, a transcription factor that subdivides the early fly embryo into presumptive muscle, skin, and nerve tissues (Kanodia et al, Development, 2011).
Our paper provides a practical definition of the range of a morphogen gradient, a statistical procedure for estimating this range, a demonstration of this procedure in practice, and several independent experimental tests of derived estimates. From the biological standpoint, the range of a gradient can be viewed as the distance over which it acts as a spatial regulator of cell responses.
Consider a common scenario in which the level of a morphogen decays from the maximal level at the point of morphogen production to the basal level at the position most distant from the peak of the gradient. As a practical definition of the spatial range of a gradient, we propose to use the distance from the peak value at which the level of the measured signal first becomes indistinguishable from the baseline.
This position can be estimated as follows. First, by measuring morphogens gradients in a collection of embryos, one can construct an empirical distribution function for the morphogen levels at multiple positions within the tissue. Second, based on these distribution functions, one can compare the mean of the morphogen level at a specific location to the baseline value. The larger the distance between from the position of the peak of the gradient, the smaller is the difference from the baseline value. The range is defined is the largest distance at which the means of the two distributions (at a current position and at the position most distant from the peak) are different from each other.
Clearly, this definition of the range leads to an estimate that is affected by the variability in the analyzed dataset. The larger the variability, the smaller is the estimated range. Since some sources of the observed variability come from the experimental procedure, such as uncertainty associated with determining the developmental stage, our estimate for the range is conservative. In other words, the true range of the gradient is actually larger than that predicted by our analysis.
Following this procedure, the range of the nuclear Dorsal gradient is estimated around 2/3 of the dorsoventral axis. As an independent estimate for the range of this gradient, we characterized the spatial extent of its transcriptional effects. For this, we use short gastrulation (sog), a well-studied transcriptional target of Dorsal and quantified the spatial pattern of its expression within the tissue. Remarkably, the spatial extent of sog expression came out to be very close to our estimate of the spatial range of Dorsal, which acts as a direct regulator of sog.
One of the main outcomes of our studies is the conclusion about the size of the dataset needed to estimate of the range of a spatially distributed signal. An accurate estimate can be obtained based on a dataset from ~40 embryos, which is within the reach for a large number of experimental systems. When combined with the fact that our computational procedures are easy to implement and require only the basic knowledge of statistics, we expect that our approach should be applicable in multiple developmental events controlled by morphogen gradients.
![]() Kanodia, J., Kim, Y., Tomer, R., Khan, Z., Chung, K., Storey, J., Lu, H., Keller, P., & Shvartsman, S. (2011). A computational statistics approach for estimating the spatial range of morphogen gradients Development, 138 (22), 4867-4874 DOI: 10.1242/dev.071571
Kanodia, J., Kim, Y., Tomer, R., Khan, Z., Chung, K., Storey, J., Lu, H., Keller, P., & Shvartsman, S. (2011). A computational statistics approach for estimating the spatial range of morphogen gradients Development, 138 (22), 4867-4874 DOI: 10.1242/dev.071571


 (11 votes)
(11 votes)