Data manipulation? It’s normal(ization)!
Posted by Joachim Goedhart, on 25 June 2019
In a previous blog, I have highlighted several ways to visualize the cell-to-cell heterogeneity from time-lapse imaging data. However, I have ignored that data is often rescaled in a way that reduces variability. For time-lapse imaging data, it is common to set the initial fluorescence intensity to 1 (or 100%). As a consequence, any changes in the fluorescence are displayed as deviations from unity. This rescaling method is often indicated as “normalization”. A definition of normalization would be “the rescaling of data to facilitate comparison”. Below, several methods of data normalization are highlighted. The examples use experimental data from fluorescence spectroscopy or imaging but rescaling methods are widely applied to all sorts of data.
Part 1: Normalization by initial value
Normalization based on the initial signal is useful when perturbations of a steady state are studied. In this type of experiment, the unperturbed system is monitored for some time, after which the perturbation (e.g. addition of an agonist or optogenetic stimulation) is applied. The initial signal, or more strictly, the signal at t=0, is defined as I0 (also often abbreviated as F0). Instead of this strict definition, we often use the signal from a ‘baseline’. The baseline is the average signal that is acquired in the period before the stimulation. By using an average, instead of a single value, we obtain a better estimate of I0. There are several ways to use the I0 to perform normalization, as will be discussed below.
Fold change: Division by initial value (I/I0)
One way to normalize fluorescence intensity data from time-lapse imaging is by dividing the intensity at every time-point (I) by the fluorescence intensity of the first time point (I0). One application of this normalization method is for analyzing and comparing photostability. The intensity at t=0 is set to 1 (or 100%) and the effects of illumination on the intensity (usually a reduction according to an exponential decay) are followed over time. The initial fluorescence is set to 1 to get rid of the absolute intensity that reflects the protein concentration. This is acceptable, since photobleaching rates do not depend on initial concentration of intensity.
Another application is in detecting changes in location of fluorescent biosensors (Postma et al 2003). The fluorescence signal in the cytoplasm is monitored over time and a reduction in the signal reflects depletion from the cytoplasm and accumulation elsewhere. To account for different expression levels between cells, these data are often normalized to the baseline value, setting the initial fluorescence to 1. The normalization enables the comparison (or averaging) of the data from different cells (this would be difficult or impossible if the data are not treated in this way). A similar normalization method is used to average and compare the response of FRET based biosensors (Reinhard, 2017)
Figure 1: Data from a time-lapse imaging experiment that measures the fluorescence intensity of the calcium sensitive biosensor GCaMP6s in HeLa cells. At t=40s, the cells were stimulated with histamine which results in an increase of intensity, reflecting an elevated calcium concentration. The raw data is shown on the left, with I0 and Imax indicated in the graph. The effect of two normalization methods, showing ’fold change’ and ‘relative intensity’ is shown in the middle panel and right panel.
Difference: subtraction of initial value (I-I0)
In the previous method, the fold change is obtained by dividing the data by I0. Instead of this relative change, the absolute change in intensity can be determined. To this end, the intensities are subtracted by the intensity at t=0 (I0). The same considerations for I0 apply. This normalization is used when the absolute difference from the baseline is of interest.
Relative change: the difference divided by the initial fluorescence (ΔI/I0)
This rescaling method can be applied to data from timelapse experiments, to show the relative change compared to the baseline. Using the relative change has the advantage (just like the fold change) that the initial intensities are equal and therefore can be used to average multiple measurements.
The relative change is commonly used for the display of calcium changes measured with a fluorescent biosensor (figure 1). In some cases it is multiplied by 100 to depict the change as a percentage (relative to I0). The rescaling method for the ‘relative change’ is related to the method for the fold change that was treated before. To understand the relation we can rewrite ΔI/I0:
ΔI/I0 = (I-I0) / I0 = (I/I0) – 1
Since I/I0 is defined as the ‘fold change’, the ‘relative change’ normalization is essentially the same as I/I0, but offset by one. Knowing this relationship, it is straightforward to convert data between the ‘fold change’ and ‘relative change’.
Z-score: the difference divided by the standard deviation of the initial value ((I-I0)/SD(I0))
The standard deviation of the baseline reflects the variability of the initial signal. The change in intensity relative to this variability is the Z-score. The Z-score indicates the number of standard deviations that the signal differs from the initial signal (Segal 2018) and reflects how well signals can be detected. For instance, if there is a large standard deviation, a small change in the signal will be hard to detect. The Z-score is of interest for assay development, where the detection of an effect needs to be optimized.
Part 2: Normalization by minimal and/or maximal values
The previous normalization methods all use I0 for the normalization. This is useful for data from timelapse experiments. Other normalization methods use other values, for instance Imax and/or Imin. Two methods will be treated below.
Set maximum to 1: I/Imax
Normalization of values based on the maximal value is common for the rescaling of absorbance and emission spectra from spectroscopy (for examples see Mastop et al, 2017). The shape of a spectrum is usually the feature of interest instead of their amplitude. The normalization is done by dividing each value by the maximal value, to enable the comparison of spectral shapes.
Rescale between 0 and 1: (I-Imin)/(Imax-Imin)
When data is rescaled based on the maximum and minimum value, the minimal value is set to zero and the maximal value is set to unity. As a consequence, the information about the absolute values is lost. Still, the shape of the curve is kept. Therefore, this rescaling method facilitates the comparison of the shapes of the curves. This method is applied when changes in the signal are relevant, but their absolute values are not. It is a valuable transformation when dynamics are compared. It is also used for dose-response curves, where the midpoints (value on the y-axis that is exactly between the minimal and maximal value) of different conditions are compared. After rescaling, the midpoint corresponds to a value of 0.5 on the y-axis.
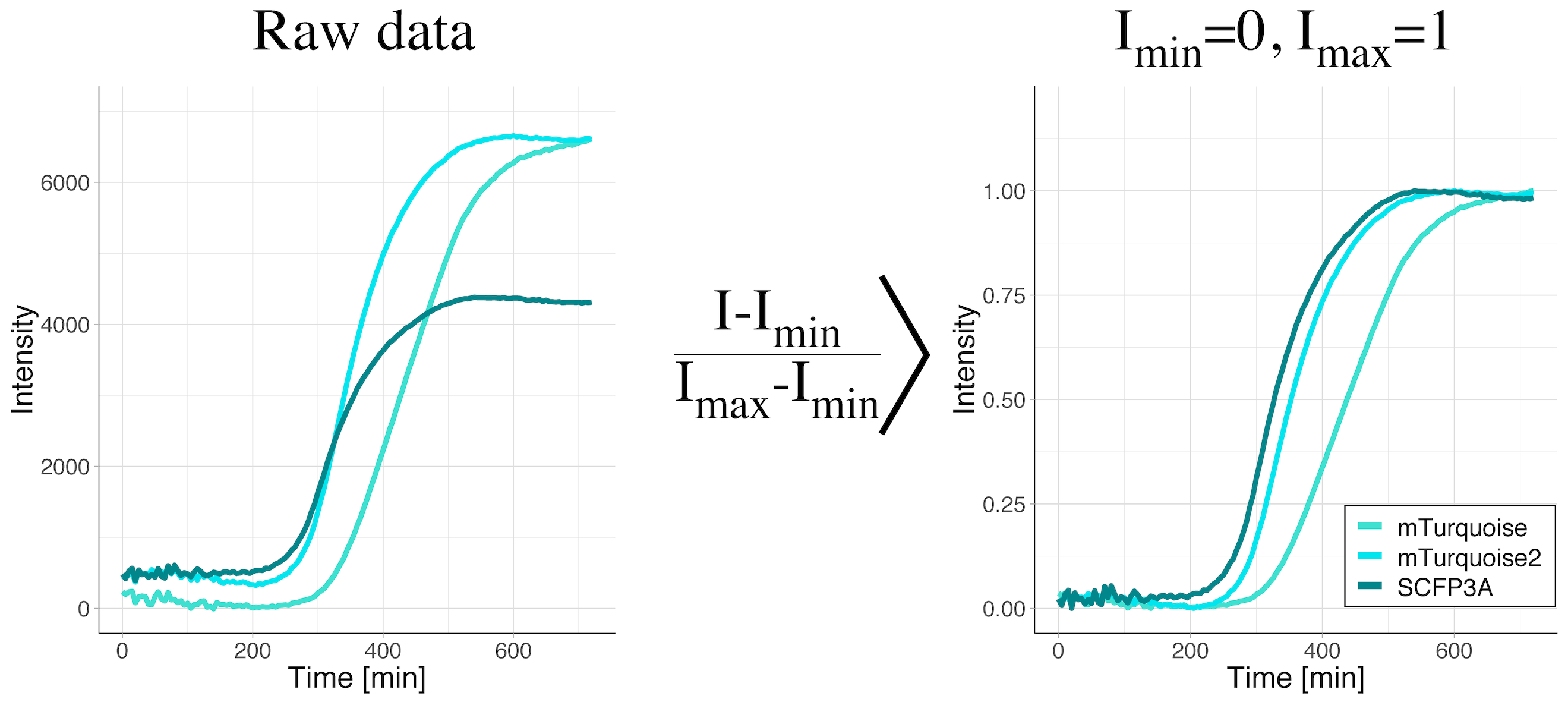
We have used this type of rescaling to compare maturation kinetics across different fluorescent proteins (Goedhart, 2012). The rescaling gets rid of the differences in fluorescence intensity and enables direct visual comparison of maturation kinetics (figure 2).
Figure 2: Data from a time-lapse measurement of the fluorescence intensity of bacterial cultures to evaluate fluorescent protein maturation rates. The bacteria were producing the cyan fluorescent proteins SCFP3A, mTurquoise or mTurquoise2. The raw data shows a clear difference in the fluorescence levels (left panel). Only after rescaling the intensity between the minimal and maximal values (right panel), the difference in maturation rates become visible. The maturation rate increases in the order mTurquoise < mTurquoise2 < SCFP3A.
Final Words
Data normalization is a meaningful data manipulation method as it facilitates comparisons. It should be realized however, that information is lost by the data rescaling. Whether this reduction of information is acceptable should be carefully evaluated. For instance, we have seen cases where a cellular response to a biosensor depended on the absolute intensity (protein concentration). Hence, it is advisable to examine both normalized and raw data for trends.
Implementation
Data normalization is readily performed by different applications and we have used R and microsoft Excel. The rescaling methods discussed here are implemented in the webtool PlotTwist: https://huygens.science.uva.nl/PlotTwist/. The R code for the webtool is available on Github.
Shout out
I like to thank all colleagues for the discussions (IRL or in the twitterverse) that helped to improve the PlotTwist webtool and especially the people that contributed suggestions for normalization methods.



 (13 votes)
(13 votes)
are standard deviation and error calculated from the normalized data? Or are they calculated from the original data then applied to the normalized data?
We quite often normalize based on initial fluorescence levels, for instance to compensate for different levels of expression. Subsequently, we calculate the SD and or 95%CI.
Hope this answers your question.