How to color a lizard: from developmental biology to physics to mathematics
Posted by LANE, on 7 June 2017
One of the research topics in Michel Milinkovitch’s laboratory (https://www.lanevol.org) at the University of Geneva (Switzerland) is to understand how squamates (lizards and snakes) generate such a tremendous variety of colours and colour patterns.
Colours
The colour of a lizard’s patch of skin is generally the result of the combination among structural and pigmentary elements found in various types of chromatophores(1-5). Pigmentary colours are produced by brown/black melanins in melanophores, as well as by yellow and red pteridines/carotenoids in xanthophores and erythrophores, respectively. On the other hand, structural colours are produced by light interference in iridophore cells containing layers of guanine nanocrystals(5): the wavelengths specifically reflected by these periodic structures is a function of the mean distance between successive layers of guanine nanocrystals — the longer the distance, the longer the wavelengths that are reflected. For example, many species of reptiles and amphibians are green despite that their skin does not contain any green pigment! They produce their chlorophyll-matching colour in a more sophisticated way(4): a layer of iridophores selectively reflects most of the incoming green and blue wavelengths but a layer of yellow pigments absorbs blue. As all other wavelengths of the visible range (yellows, oranges, and reds) go through the skin (and are absorbed by deeper tissues), the only colour that bounces back from the skin is pure bright green(4), as in day geckos (Fig. 1a).
The Milinkovitch lab also discovered that chameleons change colour by manipulating structural colours rather than by dispersion/aggregation of pigment-containing organelles within chromatophores. Indeed, combining microscopy, videography, RGB photometry and photonic band-gap modelling, they showed that chameleons shift colour through active tuning of a 3D lattice of guanine nanocrystals within a superficial layer of dermal iridophores(5). In other words, chameleons manipulate light interference by changing the distance among their nanocrystals of guanine. Take an adult male panther chameleon. In its cryptic state, it is green for the same reason as the Phelsuma lizards: its dermal iridophores reflect green and blue, and the latter is being absorbed by a yellow pigment. But if another mature male enters its territory, the two animals increase the distance between the nanocrystals within their iridophores … such that they both turn yellow or orange or red to become as visible as possible and impress each other (Fig. 1b and link to YouTube videos). This usually suffices for one of the two males to give up…otherwise they will start a physical fight.
These studies provided some new answers but also opened many new questions. How do iridophores generate and spatially organise nanocrystals? What is the cellular mechanism involved in the tuning of the distance among nanocrystals in iridophores of chameleons when they change colour? Milinkovitch is now teaming up with biochemists/cell biologists such as Marcos Gonzalez-Gaitan for investigating these questions.
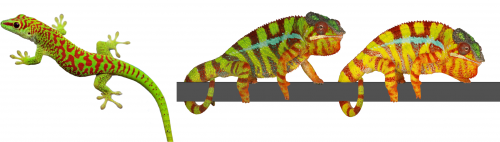
Colour change in chameleons YouTube playlist.
Colour Patterns
Animals display colours, but they often additionally exhibit colour patterns, i.e., symmetry-breaking regularities (stripes, spots, tessellations, meanders, and labyrinths) that result from short-range and long-range interactions among chromatophores(6-11). At the macroscopic scale, these dynamical processes obey reaction-diffusion (RD) equations discovered by the mathematician Alan Turing(12-14). Strikingly, the formation of skin colour in the ocellated lizard (Timon lepidus) seems to conflict with this RD framework as skin scales, rather than individual chromatophore cells, establish the pattern. Indeed, the brown juvenile lizard gradually transforms its skin colour as it ages to reach an intricate adult labyrinthine pattern where each scale is either green or black (Fig. 2).
But why would the pattern form at the level of scales, rather than at the level of biological cells? This is the questions that the Milinkovitch team solved recently, as reported recently in the journal Nature(15).
T
o tackle this question, two PhD students, Liana Manukyan (computer scientist) and Sophie Montandon (developmental biologist), followed individual lizards during three to four years of their development from hatchlings crawling out of the egg to fully mature animals. For multiple time points, they reconstructed the geometry and colour of the network of scales on three animals by using R2OBBIE-3D (YouTube playlist), a very high resolution robotic system(16) developed previously in the Milinkovitch laboratory by a physicist PhD student: Antonio Martins.
R2OBBIE-3D YouTube playlist
R2OBBIE-3D allows to reconstruct the 3D geometry and colour texture of objects up to 1.5 meters with a resolution of … 15 microns ! The Swiss team then set up a software pipeline that allowed them to automatically detect scales on each animal at each time point and match these networks. This was not a trivial task because the size of the animal, the positions of its body parts, and its skin pattern all change from scan to scan. Fortunately, the number of scales is invariant for a given individual throughout its life. This analysis indicated that the brown juvenile scales change to green or black then, surprisingly, continue flipping colour (between green and black) during the life of the animal (Fig. 3).
This very strange observation prompted Milinkovitch to suggest that the skin scale network forms a so-called ‘Cellular Automaton’. This esoteric computing system was invented in 1948 by the mathematician John von Neumann. Cellular automata are lattices of elements in which each element changes its state (here, its colour, green or black) depending on the states of neighbouring elements. The elements are called cells but are not meant to represent biological cells; in the case of the lizards, they correspond to individual skin scales. These abstract automata were extensively used to investigate computing systems and to model natural phenomena, but the Geneva team discovered what seems to be the first case of a genuine 2D automaton appearing in a living organism. Analyses of the four years of colour change allowed to confirm Milinkovitch’s hypothesis: the scales were indeed flipping colour depending of the colours of their neighbour scales. Computer simulations implementing the discovered mathematical rule generated colour patterns that could not be distinguished from the patterns of real lizards.
How could the interactions among pigment cells, described by Turing equations, generate a von Neumann automaton exactly superposed to the skin scales? The skin of a lizard is not flat: it is very thin between scales and much thicker at the center of them. Given that Turing’s mechanisms involves movements of cells, or the diffusion of signals produced by cells, Milinkovitch understood that this variation of skin thickness could impact on the Turing’s mechanism. Liana Manukyan, but also Anamarija Fofonjka, a third PhD student in Milinkovitch’s team, then performed computer simulations and saw a cellular automaton behaviour emerge, demonstrating that the development of Cellular Automata as computational systems is not just an abstract concept developed by John von Neumann, but also corresponds to a natural process generated by biological evolution.
However, the automaton behaviour was imperfect as the mathematics behind Turing’s mechanism and von Neumann automaton are very different. Milinkovitch called in Stanislav Smirnov, Professor of mathematics at the University of Geneva. Stanislav was awarded in 2010 the Fields Medal (the equivalent of the Nobel Price in Mathematics). Before long, Smirnov derived a so-called discretisation of Turing’s equations that would constitute a formal link with von Neumann’s automaton. Anamarija Fofonjka implemented Smirnov new equations in computer simulations, obtaining a system that had become un-differentiable from a von Neumann automaton (Fig. 4). The highly multidisciplinary team of researchers had closed the loop in this amazing journey, from biology to physics to mathematics.
Bibliography
1. T. Kuriyama, K. Miyaji, M. Sugimoto, M. Hasegawa, Zoological Science 23, 793-799 (2006).
2. J. Cote, S. Meylan, J. Clobert, Y. Voituron, J Exp Biol 213, 2116-2124 (2010).
3. S. L. Weiss, K. Foerster, J. Hudon, Comp Biochem Physiol B Biochem Mol Biol 161, 117-123 (2012).
4. S. V. Saenko, J. Teyssier, D. van der Marel, M. C. Milinkovitch, BMC biology 11, 105 (2013).
6. M. Inaba, H. Yamanaka, S. Kondo, Science 335, 677 (2012).
7. H. G. Frohnhofer, J. Krauss, H. M. Maischein, C. Nusslein-Volhard, Development 140, 2997-3007 (2013).
10. A. Fadeev, J. Krauss, H. G. Frohnhofer, U. Irion, C. Nusslein-Volhard, Elife 4, (2015).
11. D. S. Eom, D. M. Parichy, Science 355, 1317-1319 (2017).
13. A. Gierer, H. Meinhardt, Kybernetik 12, 30-39 (1972).
14. S. Kondo, T. Miura, Science 329, 1616-1620 (2010).
16. A. F. Martins, M. Bessant, L. Manukyan, M. C. Milinkovitch, PloS one 10, e0126740 (2015).
(3 votes)
Loading...