This summer I was privileged with the opportunity to conduct research at the Francis Crick Institute in the Mathematical and Physical Biology Laboratory, which studies how structure and organisation emerge in living systems using mathematics and computational analysis.

Integral feedback control is a type of control strategy used in engineering or automation that utilises accumulated error over time to make gradual adjustments to a system’s output signal. As a mechanical engineering student, it would be more common for me to see integral feedback control in thermostats, cruise control systems in cars, or other mechanical systems where a system must be restored back to an equilibrium without oscillating. However, the integral feedback control mechanism is also observed in multiple biological systems, including in one model used to explain morphogen gradient scaling.

Morphogens are signalling molecules that are produced in a restricted region of a tissue and spread away from their source via diffusion to form a concentration gradient [1]. The shape of the morphogen gradient dictates cell fate in a concentration-dependent manner (Fig. 1a). Although individuals of the same species can differ in size during development, their proportions remain approximately constant. This requires that the length scales associated with morphogen gradients increase proportionally with system size, and is referred to as morphogen gradient scaling [2].

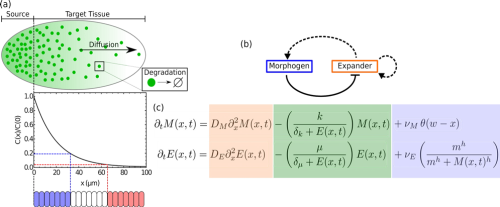
Figure 1: (a) Schematic of morphogen-mediated patterning. Morphogens diffuse into the tissue from a source region on the left, and their diffusion and degradation forms a concentration gradient. Different morphogen concentrations result in different cell fates. (b) Schematic of a novel version of the expansion-repression model, showing that morphogen signalling represses the production of the expander and that the expander in turns expands the morphogen gradient. (c) The equations describing the evolution of the morphogen and expander concentrations according to the expansion- repression model in (b) with respect to space (x) and time (t). The diffusion terms (orange) include the diffusion constants DM and DE, the degradation terms (green) include the degradation rate constants and k and μ, and the production terms (blue) include the production rate constants νM and νE. h is a Hill coefficient, θ ( x ) is the Heaviside step function, and δk , μand m are constants.

One mechanism that may be used to achieve morphogen gradient scaling utilises an integral feedback control mechanism, and is termed the “expansion-repression” model [2]. In this case, the shape of the morphogen concentration gradient that prescribes patterning is regulated by a diffusible molecule called the “expander”, which aids the spreading of morphogens either by enhancing their diffusion or by protecting them from degradation (Fig. 1b). In turn, the production of expander molecules is repressed by morphogen signalling. This morphogen-expander feedback is the same type of integral control feedback observed in other biological and engineering systems. The behaviour of morphogen and expander molecules can be expressed mathematically (Fig. 1c), and these equations can be solved numerically. Simulations indicate that the novel formulation of the expansion-repression model shown in Fig. 1b can become unstable at certain system sizes as a result of the integral feedback control mechanism, which results in oscillations in the morphogen concentration that continue forever.

During my time with the Mathematical and Physical Biology Laboratory, I adapted code written in Julia to investigate the instabilities that arise for a morphogen-expander system (Fig. 1b,c) at different system sizes. I calculated the critical length of the system, which is the system size below which normal patterning can be achieved for biological systems, and above which the system becomes unstable. In addition, by varying system parameters such as the diffusion, degradation rate or production rate constants for either the morphogen or expander molecules, we began to investigate what may cause the morphogen-expander system to become unstable. For example, increasing the morphogen diffusion constant causes the critical length of the system to vary non- monotonically (Fig. 2). This means that for certain values of the diffusion constant the system becomes unstable at smaller system sizes, and that there is a value of the diffusion constant for which the system is at its least stable. Similar changes can be observed in the rate at which the system approaches the instability, characterised by the value of the critical exponent β (Fig. 2).

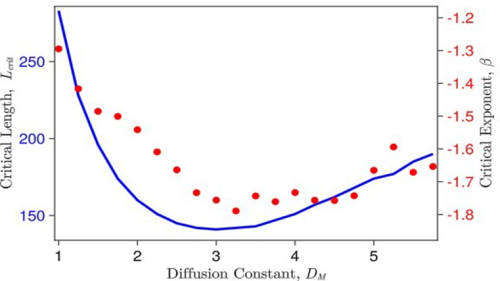
Figure 2: The critical length for the morphogen-expander system decreases rapidly with increasing morphogen diffusion constant until it reaches a minimum value, then it increases steadily. This suggests that there is a value of the diffusion constant for which the system is at its least stable. The critical exponent, β , tends to follow a similar trend.

This project has allowed me to build on my skills in programming and data analysis, as well as gain a better understanding of essential research skills such as presenting research and keeping a record of my learning. I am immensely grateful to have had the opportunity to work with a diverse range of scientists, including both biologists and physicists. I enjoyed this diversity and how fascinating this made lab meetings. It was incredible to see how people from different academic backgrounds come together to explore scientific problems. This has really motivated me to pursue similar interdisciplinary research in the future.

I would like to thank Dr Lewis Mosby for his incredible supervision, as well as Dr Zena Hadjivasiliou and the entire Mathematical and Physical Biology Laboratory for their support and for creating such a fascinating experience.

I look forward to continuing a career in research and I urge other undergraduates to apply to the Francis Crick Institute summer student training programme. I would like to thank the Francis Crick Institute for hosting me and the Medical Research Foundation Rosa Beddington Fund for supporting my project.

https://www.linkedin.com/in/andile-hlongwane-712a70213/

References

• – Jan L. Christian. Morphogen gradients in development: from form to function. Wiley Interdiscip. Rev. Dev. Biol., 1(1):3-15, 2012.
• – Danny Ben-Zvi and Naama Barkai. Scaling of morphogen gradients by an expansion- repression integral feedback control. Proc. Natl. Acad. Sci. U.S.A., 107(15):6924–6929, 2010.

(No Ratings Yet)

Loading...