Precision by design: Setting boundaries in patterning
Posted by Edgar Herrera Delgado, on 1 March 2021
Developmental patterning is an essential process for multicellular development, as it drives the cell-fate decisions that determine an organism’s body plan. One of the aspects that has fascinated me is the accuracy and reliability of patterning. The accuracy is particularly intriguing because we know this happens in spite of the natural stochasticity that can disrupt biological processes such as tissue patterning. So how do biological systems consistently produce the same pattern with sufficient robustness such that the embryo forms correctly (nearly) every time? This question has been explored by many over the years and several strategies for enhancing developmental robustness have been described. These strategies include redundant gene activation in case of perturbations, cell sorting, preferential adhesion or modifications to the morphogen levels. However, in our recent study we found yet another mechanism, one that functions at a different level of the system, to boost the robustness and the accuracy of tissue patterning.
The study arose as a collaboration between myself, mostly a theoretician at the time, and a fellow student in the lab, Katherine, an experimental biologist (Exelby K et al, 2020). We were studying the vertebrate neural tube. This is often held up as a prime example of a system patterned by a morphogen gradient through positional information in the manner proposed by Lewis Wolpert. My lab had spent many years dissecting the mechanism of neural tube patterning and recent work had been focusing on how signalling gradients are interpreted by a gene regulatory network (GRN) composed of cross-repressive transcription factors (TFs) (Fig. 1 left). A striking feature of neural tube patterning is the sharpness of the borders between gene expression domains that pattern its dorsal-ventral axis. The mechanisms that explain this precision are not well understood. My supervisor, James Briscoe, encouraged Katherine and me to think about some old observations that mutant mice lacking the transcription factor Pax6, one of the genes in the GRN, seemed to disrupt the precision of a boundary between two cell types, the so-called p3 and pMN domains. We repeated these experiments and confirmed that in embryos lacking Pax6 there was a lot more intermixing of cells at this boundary than in wild-type embryos. Importantly, the cell types of each domain were not altered, as the expression of the other components of the GRN remained the same. Furthermore, there is no obvious evidence of a change in cell mobility or adhesion downstream of Pax6. This encouraged us to explore whether this imprecision might be explained by the GRN and how that could happen.
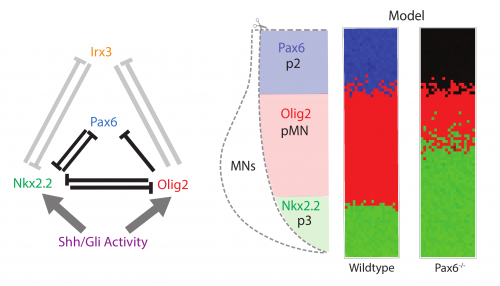
We took a mathematical model previously developed in the lab that captures the patterning of the neural tube (Cohen M et al, 2014) and the effects of the various transcription factor knockouts on the patterning. I adapted this model by adding stochasticity, to account for noise in gene expression and degradation. I was pleasantly surprised that just by adding gene expression noise, the model mimicked the loss of precision in patterning seen in the Pax6-/- knockout (Fig. 1 right).
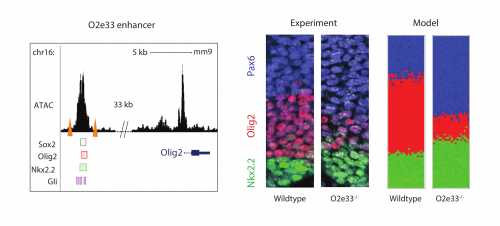
Investigating further, I found that the model suggested altering interaction strength between some of the transcription factors in the GRN could also produce imprecise boundaries. Serendipitously (or perhaps it was good planning), Katherine was experimentally deleting enhancers of some of the transcription factors in the GRN, reasoning that this could alter interaction strengths. She found that when she removed an enhancer for the Olig2 transcription factor (we termed the enhancer O2e33) (is removed), the precision of the p3 and pMN domain was reduced (Fig. 2). The loss of the enhancer did not change the cell types that were generated, it was just that they were more intermixed than normal at the boundary. Just as for the Pax6 mutant, this suggested that corrective mechanisms, such as differential adhesion, probably didn’t explain the precision. Instead, it was consistent with the predictions of the model I had been developing and indicated that the dynamics of gene expression conferred by the GRN play an important role in boundary precision.
So why was this? I set to use the model to understand how the GRN affects boundary precision and I found that the key element was the ease at which one cell type could transition to another. At the boundary between the two domains, the system is bistable (either pMN or p3). Close to this boundary, all cells that achieve a p3 state were previously in a pMN state and switched from pMN through random fluctuations to become p3 (Fig. 3). In the WT system, cells away from the boundary quickly become unable to transition between states by random fluctuations. However, when I simulated cells in the mutant embryos with a modified GRN, I saw that cells retained the ability to transition from pMN to p3 a greater distance away from the boundary and this results in a larger heterogeneous region and thus an imprecise boundary (Fig. 3).
Inspired by the explanation provided by our model, we explored how common it is that a GRN can favour a precise boundary and which networks can do this. Using a computational screen, I systematically explored all possible two and three-node networks that could form networks in response to a graded input and found a consistent pattern. This screen generated many networks that were able to produce sharp boundaries. Looking at these high precision networks, I realised there were two underlying mechanisms, one of which was identical to that used by the neural tube GRN (a detailed explanation is in the paper (Exelby K et al, 2020)).

These findings suggest that many real biological networks that produce boundaries appear to be more complex than might be expected, because it allows them to generate sharper boundaries. Indeed, when we examined other networks that regulate patterning through a morphogen signal such as the Drosophila GAP genes or the Drosophila eye disc, we found examples of our high precision networks in each case. The results suggest that there may be a selection of these motifs to favour precision in developmental patterns.
In summary, we found a mechanism by which GRNs simultaneously pattern a tissue and ensure the robustness of such pattern. The precision arises from the structure of the network and is a nice example of an emergent behaviour – it is a consequence of the interactions between the components in the network. We termed this ”precision by design” to reflect the fact that the sharpness of the boundaries was encoded in the GRN. I was delighted that the modelling helped us make experimental predictions and provided an explanation for the results that would otherwise have been opaque. It would not have been easy to pinpoint the mechanism without the years of work from previous theoreticians and experimentalists, allowing me to build onto a well constrained model and develop the project further at the interface between fields. Perhaps most importantly for me, the project really brought home how biological understanding emerges from projects that fully integrate experiments and theoretical modelling. I‚ have now started my post-doc working on cell fate decisions in pre-implantation embryos in the lab of Jean-Léon Maître at Institut Curie. Here, I have started lab work for the first time since my Bachelors degree, and am keen to continue incorporating theory with experiments to tackle interesting question.
Cohen, M, Page, KM, Perez-Carrasco, R, Barnes, CP, & Briscoe, J (2014). A theoretical framework for the regulation of Shh morphogen-controlled gene expression. Development, 141(20), 3868–3878.


 (12 votes)
(12 votes)
I used to get confused with math models and how one can use them to make prediction in the behavior of biological responses and phenomena. This piece is written with such clarity that bridges math models and experimental biology.
Thank you