Sensing and making sense of clonal fragmentation in developing tissues
Posted by SRulands, on 23 March 2018
Steffen Rulands and Benjamin Simons
A discussion of our recent paper: Rulands S et al., Universality of clone dynamics during tissue development. Nature Physics | doi:10.1038/s41567-018-0055-6
Often, the most enjoyable research projects are the ones that were never planned; and so it was with the current study.
In developmental biology, genetic lineage tracing methods have become a standard tool to interrogate the lineage potential and fate behaviour of cells [1]. By activating fluorescent reporter genes in individual cells, qualitative and quantitative methods have been defined to translate the size distributions of marked cells and their progeny – clones – into information on the statistical fate behaviours of constituent cells [2]. These approaches have led to important insights into the dynamics and functional behaviour of stem cells and progenitors during the development, maintenance and regeneration of tissues, as well as the dynamics of tumour growth during cancer initiation and progression.
Unlike continuous in vivo live-imaging approaches [3], the interpretation lineage tracing data, based on the analysis of fixed samples, can be confounded by uncertainties in the history of clonal evolution: First, there is a question of whether the tracing assay targets a single (functionally equivalent) cell population, or whether there is heterogeneity within the induced cell fraction. Second, there is an intrinsic ambiguity in the lineage reconstruction since multicellular clones can typically be generated from a multitude of potential lineage trajectories: Different combinations and permutations of cell divisions leading to symmetric and asymmetric fate outcomes can generate clones of the same size and cell composition. Fortunately, to a degree, both problems can be mitigated post hoc by the nature of the clonal dynamics itself!
Previously, research by our group and others have shown that, while the short-term dynamics of labelled progenitors may be highly complex, in the long-term, the size distribution of clones anchored in equipotent cell populations typically converge to rigid “scaling” behaviours in which the chance of finding a clone larger than some multiple of the ensemble average becomes unchanging over time [4]. Indeed, in self-renewing adult tissues, the constraint of homeostasis limits strongly the variety of scaling distributions, so that information on cell fate behaviour can be recovered “rigorously” from the functional form of the scaling distribution.
However, the utility of these methods is heavily reliant on the integrity of clonal assignments; and therein lies the rub! During development, and in the course of adult tissue turnover, cell rearrangements due to active cell migration, or serial rounds of cell loss and replacement, can lead to the fragmentation or merger of clones, corrupting the data and, potentially, misleading efforts to interpret the underlying clonal dynamics. Yet, in a lineage tracing approach based on the analysis of fixed samples, we can’t know what were the individual histories of clones and their fragments. Developments of multicolour lineage tracing strategies, based on the “brainbow” or confetti reporter constructs, can mitigate the potential for such effects. However, in the context of tissue morphogenesis or tumour development, large-scale cell rearrangements caused by tissue remodelling can lead to the long-distance segregation of clonal fragments rendering the task of clonal reconstruction potentially infeasible. Worse, confronted with such challenges, many researchers may feel inclined to abandon attempts to reconstruct putative clones dispersed across the three-dimensions of a solid tissue and instead to characterize the size of a clone by its intersection with a thin section of tissue – “surely a rough indication of the complete clone size…?”
Unfortunately, such hopes are dashed by the inconvenience of a mathematical riddle – the corpuscle problem – which states that, without making detailed assumptions, the distribution of three-dimensional objects cannot be recovered (even in principle) from the statistics of their random intersections [5]. Yet, for those brave enough to try to reconstruct the entirety of the clone, the situation is still treacherous since, at first sight, it is difficult to know whether the clonal assignment is faithful. With the increasing prevalence of genetic lineage tracing assays, this is the situation that prevails – with legions of researchers (and reviewers…!) questioning whether assays are clonal. Of course, statistical analyses can help. At low enough clonal induction frequency, fragmented clusters of cells can be associated with defined statistical confidence. Yet, in a developmental context, this may require organs with as few one or two clones per animal, a daunting, expensive and arguably unethical endeavour! So, can anything be done to alleviate this problem?
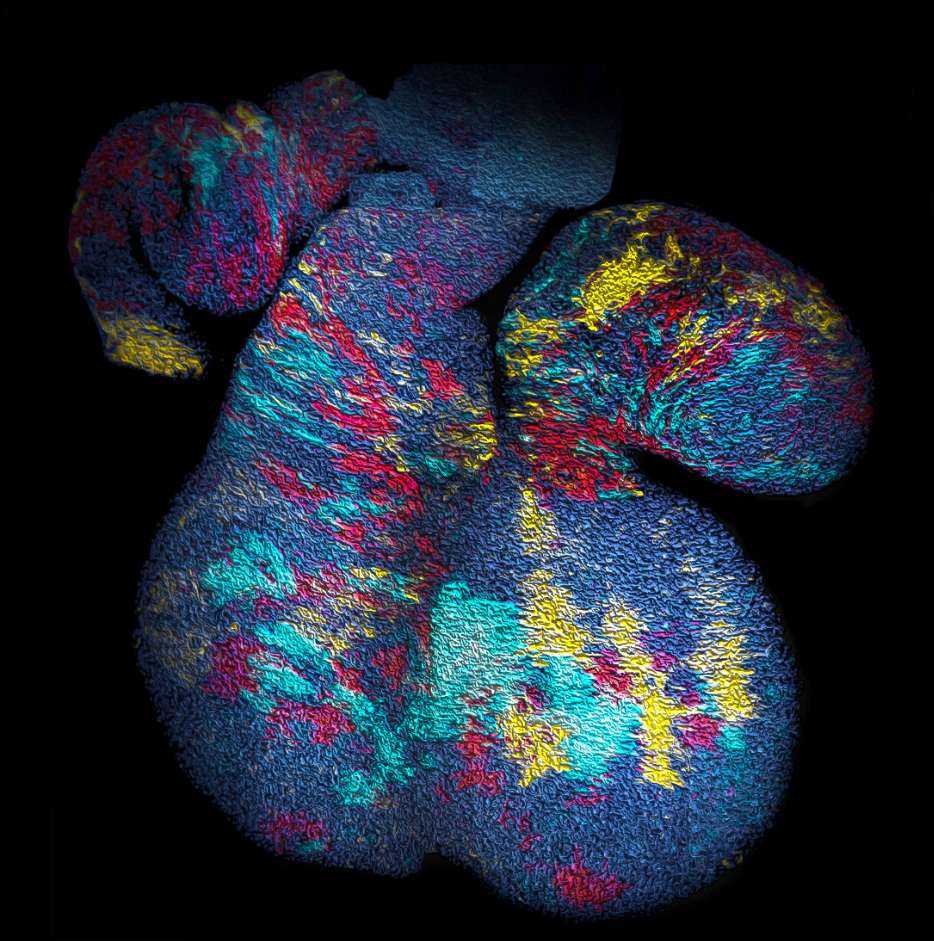
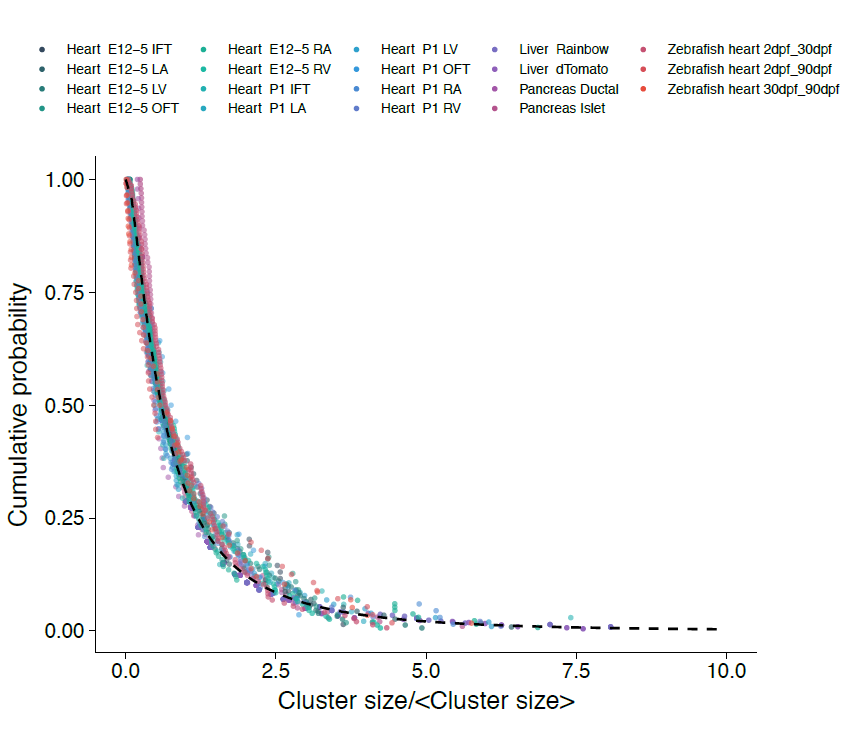
With the benefit of hindsight, we should have asked ourselves whether, in common with “true” clonal dynamics, the statistical distribution of “putative” clones could, in of itself, provide evidence that the source data was corrupted by clonal fragmentation and/or merger events. But we didn’t! Instead, we stumbled into this idea through an intriguing empirical observation. Our collaborators in the Blanpain lab at the Interdisciplinary Research Institute at the Université Libre de Bruxelles were interested in resolving the potency and proliferative potential of early Mesp1-expressing precursors in the developing mouse heart. To trace the fate of these cells, confetti labelling was induced in a fraction of Mesp1+ cells early in embryonic development, and the size and regionalization of clonal footprints were scored on the developing mouse heart (Fig. 1) [6]. Notwithstanding the corpuscle problem, we (recklessly) constructed the size distribution of clonal “fragments” on the embryonic heart and found a size dependence that was strikingly broad yet was almost void of structure (i.e. information on the underlying clonal dynamics): The average sizes of labelled fragments differed vastly between different heart compartments and time points in development – consistent with the complexity of developmental programmes during heart morphogenesis. However, to our surprise, once we divided fragment sizes by their ensemble average, the resulting rescaled probability distributions became indistinguishable between different heart compartments (Fig. 2). What could it mean…? Did this reflect a rigid growth characteristic of precursors in the maturing mouse heart – with some cells destined to proliferate and expand prodigiously while others are set to exit cycle early? Or was there a less “glamorous” explanation, at least from the perspective of our experimental collaborators…?
Of course, during development, clones are subject to numerous intrinsic and extrinsic influences that adjust cluster size: Labelled cell clusters can expand through the division of constituent cells; they can also expand through chance merger events that bring together clusters of the same hue. However, clusters can also diminish in size through cell loss – either through cell death, or by cells leaving the field of view in a sectional characterisation of cluster size; they can also diminish through fragmentation events caused by collective cell rearrangements created by larger-scale morphogenic changes or simply from stochastic forces exerted by the surrounding cells. Finally, new clusters can appear as labelled cells that are “out of frame” move into a sectional view. In short, in a model that mirrors both qualitatively and quantitatively the non-equilibrium dynamics of aerosol suspensions, the time-evolution of the distribution of labelled cell clusters conforms to a fiendishly complex set of possible processes that includes all the factors above, and potentially many more – a seemingly unpromising starting point for any analysis…
However, the rigour of statistical physics (and a little bit of hindsight) came to the rescue!! Indeed, during tissue development or turnover, constituent labelled cell clusters will stochastically expand and contract in response to the factors above. Under these conditions, the different possible influences impact on the resulting cluster size distribution to widely varying degree. Therefore, to quantify the relative contributions of these disparate processes, we employed a concept that has shaped the field of statistical physics: By progressively moving to coarser and coarser length scales, we obtained mathematical equations describing the varying contributions of different processes on these scales. We reasoned that, on the largest scales, i.e. as development proceeds, these equations then give an accurate, but reduced, description of the dynamics shaping the cluster size distributions. Notably, using an analytical approach inspired by the “renormalization group” methods of statistical physics, we could show that, over time, only the processes of clonal merger and fragmentation impact on the shape of the resulting cluster size distribution; in the parlance of statistical physics, these were the relevant operators. Crucially, if perhaps worryingly for the biologists(!), information encoded in developmental fate programmes becomes progressively erased from the cluster size record, while the emergent dynamics signals only the existence of fragmentation and/or merger events. The observed cluster size dependence was, indeed, not a reflection of some underlying fate programme, but an inevitable outcome of the collective dynamics of heart development. As a corollary, the erasure of biological information suggested that cluster size distributions obtained from lineage tracing experiments should take the same form across different biological tissues and even species. To drive home the message, we confirmed that the cluster size distributions of the developing zebrafish heart, as well as liver and pancreas, also conform to common – physicists would say “universal” – cluster size distributions with the same hallmark (in this case, log-normal) size dependence.
So far, so good, we thought; and we set off to inform the stem cell community of our findings. Not surprisingly, we found that not all experimentalists were equally enthusiastic to learn that the outcome of often challenging lineage tracing experiments might be, by design, void of biologically significant information… However, perhaps more surprisingly, we found that the very concept of universality – a rigorously defined mathematical concept at the heart of critical phenomena in statistical physics – caused additional irritation among our biological peers. More than once we were informed that “nothing in biology is universal…!” Indeed, this warning betrays something of the cultural differences that continue to divide the physical and biological science communities. While the former are trained to look for commonalities between different systems, the inherent complexity of biological systems makes it more natural to focus on differences and details.
Indeed, we believe that these observations have value both to the biology and physics community. For the former, these findings have a practical value: Although one cannot use statistical distributions to confirm positively the integrity of clonal assignments, one can at least use hallmark scaling dependences of cluster size to quantitatively and, therefore, rigorously signal when seemingly clonal data has been corrupted by fragmentation and/or merger events. At the same time, understanding the origins of universal scaling behaviour allows biologists to develop experimental strategies that can unveil the developmental programmes of labelled cells. For the physicists, the situation is more encouraging with clonal dynamics presenting yet another example of where biological systems can provide an arena in which powerful concepts from statistical physics and mathematics can find novel and practical application.
References
1. Kretzschmar K and Watt FM. Lineage Tracing. Cell. 2012; 148(1): 33-45
2. Rulands S and Simons BD. Tracing cellular dynamics in tissue development, maintenance and disease. Current Opinion in Cell Biology 2016; 43: 38-45
3. Brown S and Greco V. Stem Cells in the Wild: Understanding the World of Stem Cells through Intravital Imaging. Cell Stem Cell. 2014; 15(6); 683-686
4. Klein AM and Simons BD. Universal patterns of stem cell fate in cycling adult tissues. Development 2011; 138: 3103-3111
5. Wicksell SD. The Corpuscle Problem: A Mathematical Study of a Biometric Problem. Biometrika. 1925; 17(1): 84-99
6. Lescroart F, Chabab S, Lin X, Rulands S, Paulissen C, Rodolosse A, Auer H, Achouri Y, Dubois C, Bondue A, Simons BD and Blanpain C. Early lineage restriction in temporally distinct populations of Mesp1 progenitors during mammalian heart development.
Nature Cell Biology. 2014; 16: 829–840


 (1 votes)
(1 votes)
I found the discussion regarding universality and how it was received by biologists interesting.