BSDB Gurdon/The Company of Biologists 2019 Summer Studentship Report – Jake Cornwall Scoones

Established by the British Society for Developmental Biology in 2014, The Gurdon/The Company of Biologists Summer Studentship scheme provides financial support to allow highly motivated undergraduate students an opportunity to engage in practical research during their summer vacation. Each year, ten successful applicants spend eight weeks in the research laboratories of their choices, and the feedback we receive is outstanding. You can read accounts from previous years here. If you’re interested in applying or hosting a student in 2020, applications need to be in by the end of March.

Our tenth and final report from the class of 2019 comes from Jake Cornwall Scoones who studied developmental mechanics in the fly embryo in Bénédicte Sanson’s lab at Cambridge.

Developing force inference strategies to analyse tissue-wide stress in the Drosophila germband

Morphogenesis is an integral aspect of embryonic development, shaping collections of cells into functional tissues. Developmental mechanics aims to unravel how forces across spatial scales, from cytoskeletal processes, to junctional dynamics and inter-tissue interactions, facilitate emergent transformations in embryonic form. Analysing mechanics across scales requires a systems-level approach, where quantifying tissue-wide stress and material properties is essential. Current methods for directly measuring forces in vivo have major short-comings: methods (e.g. laser ablation) are invasive, perturbing the stress field and prohibiting extensive sampling. Non-invasive force inference approaches are useful alternatives, using segmented images of fluorescently-labelled cells to infer relative tension across each cell membrane and pressure in every cell. They do this by fitting tissue-wide tension and pressure nets to these data via the assumption of force-balance.

Focusing on Drosophila germ-band extension, a well-studied example of axis extension, I developed computational tools for non-invasive inference of stress distributions from microscopy data. These algorithms consider an epithelial sheet as a 2D curved-polygonal lattice, with edges demarcating cell membranes, and vertices defined where three cells meet (Fig. 1a). Using some simplifying physical assumptions, they use the geometries of edges at each vertex, as well as the curvatures at each edge, to infer relative pressures in every cell and relative tensions at every edge.

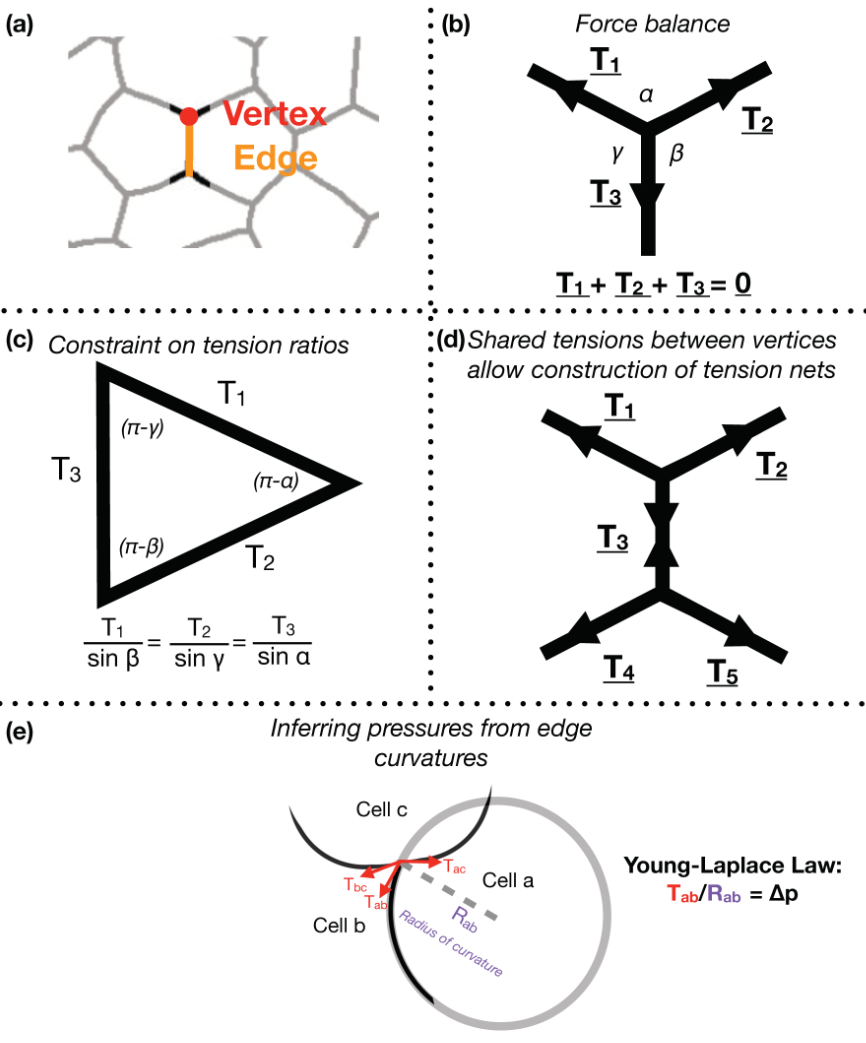
Despite the variation in computational implementation strategy, many existing force inference methods have a common underpinning logic. Specifically, they assume that the tensions at every vertex are balanced; in other words, that the system is in mechanical equilibrium (Fig. 1b). Thus given the angles that edges of a given vertex make with each other, as inferred from microscopy data, one can infer ratios of relative tensions (Fig. 1c). Further, they assume that tension is continuous across an edge, meaning relative tensions can be inferred tissue-wide (Fig. 1d). Cellular pressures can also be inferred. When edges are curved, it is assumed that the cell for which the edge is convex shows higher pressure. In fact, one can infer the pressure differential in terms of the inferred tension and the radius of curvature of that edge using the Young-Laplace law (Fig. 1e).

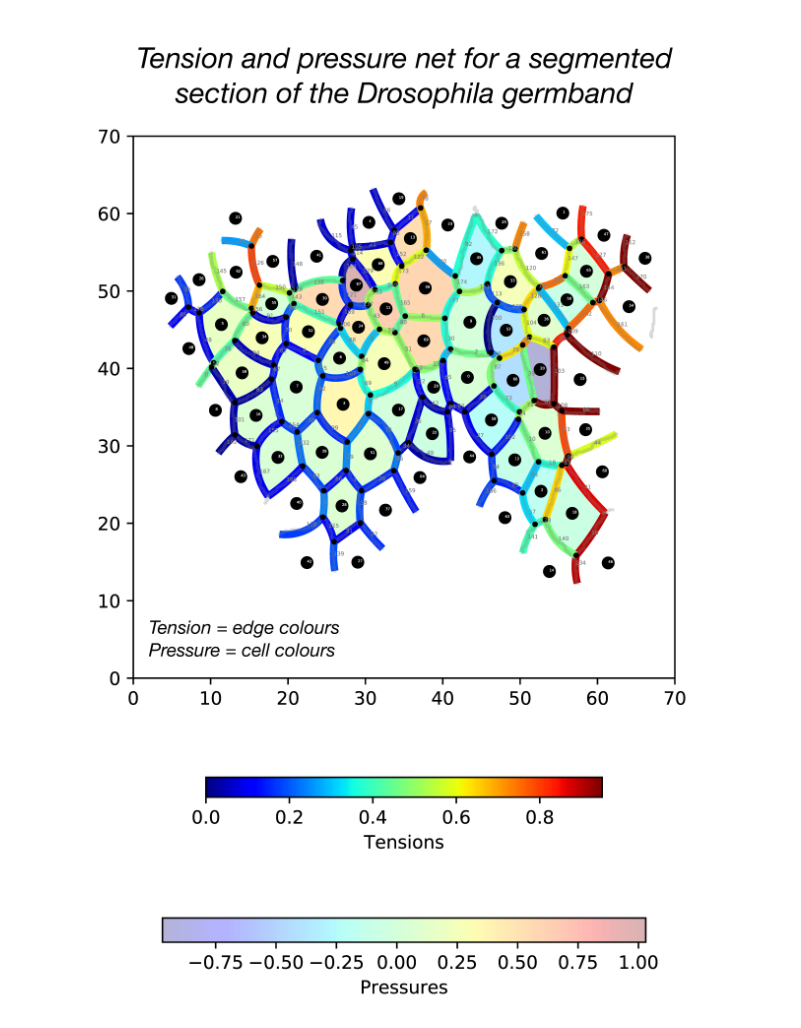
During my stay with the Sanson lab, I developed a pipeline in Python for force inference. The pipeline takes the many frames of segmented germband movies curated by the lab, uses one of several possible force inference strategies, and outputs the inferred tensions and pressures back to the lab’s wider computational workflow (Fig. 2). Given the wealth of data collected by the lab, these strategies now have immediate use in analysing global patterns of stress (indeed without the need for additional experiments), for example in characterising non-intuitive changes to stress distributions in key morphogenetic mutants (e.g. sidekick mutants, see Finegan et al 2019, PloS Biology, https://doi.org/10.1371/journal.pbio.3000522). Besides direct analyses of stress distributions, these inferences can now be used to parameterise physical models of the germband, across spatial scales. Beyond this, I have compared the various implementation strategies with regards to their concordance in predictions, and tested their relative capacities of dealing with noise in segmentation. I have also surveyed both the practical and conceptual challenges of these strategies with an intention of refining existing methodologies for faster and more accurate inference.

This project has allowed me to refine skills in programming, especially in visualisation, data processing and algorithm optimisation. I am now putting the algorithms together into a coherent and user-friendly package for use in the lab internally, but also, excitingly, to be released as an open-access resource. Further, working in Dr. Sanson’s lab also introduced me to key concepts in mechanics, situated in this biological context.

Given the highly interdisciplinary makeup of this project, supervised by Dr. Alex Nestor Bergmann (mathematician and physicist), Dr. Guy Blanchard (computational biologist), and Dr. Bénédicte Sanson (developmental biologist), I enjoyed how divergent perspectives and methodologies are brought together to solve this multi-scale problem. I endeavour to pursue similar interdisciplinary research in a PhD and beyond, carrying out both dry and wet components.

I would like to thank Dr. Alex Nestor Bergmann and Dr. Guy Blanchard for their fantastic supervision and the Sanson lab as a whole for their support and their fascinating and diverse lab meetings. I finally want to thank the BSDB for providing me the opportunity to carry out this research, and urge other undergraduates to apply to the Gurdon Studentship.