When statistical physics meets developmental biology: Predicting the structural properties of embryonic tissues from a simple cell parameter

By Bernat Corominas-Murtra and Nicoletta I. Petridou

Embryo morphogenesis is a play whose outcome is the result of a complex and delicate plot, made of balances and agreements among many actors: the execution of the genetic program, biochemical communication among cells, mechanical forces, energy consumption, geometry, cell autonomous and collective behaviours… all of them interlinked in a precise way in space and time. This process is by no means always smooth, and in some developmental stages, dramatic, sudden shifts in the properties or structure of the embryo occur.

It was precisely one of these sudden shifts that started puzzling us about three years ago during a scientific retreat in the beautiful town of Sitges, in the Catalan coast, between the groups of Edouard Hannezo and Carl-Philipp (CP) Heisenberg from IST Austria. At that time, I (Nicoletta) was a postdoc in CP’s group, and one of the targets of our research was to establish how tissue material properties change in space and time within the zebrafish embryo at the onset of morphogenesis. At this stage, the embryo is composed of a few thousand cells (the blastoderm) sitting on top of a yolk cell. The blastoderm starts spreading and engulfing the yolk, defining the onset of gastrulation. By measuring blastoderm viscosity in vivo we knew that the viscosity of the embryo tissue drops by more than an order of magnitude at the exact moment when morphogenesis starts, in a highly reproducible way. That is, in a matter of minutes, the embryo jumps from a “solid” non-deformable state to a “fluid” highly-deformable one. Right after this abrupt shift, the tissue starts recovering its viscous properties by undergoing “thickening” (in rheological terms, like a honey that thickens and loses deformability). These spatiotemporal changes in tissue viscosity are essential for correct tissue spreading at the onset of morphogenesis. As a funny coincidence, exactly on the very first day of the retreat we had just found out that our manuscript on these findings was accepted for publication (Petridou et al., 2019). Besides the celebratory mood, we were still excited and puzzled by the abrupt nature of this shift, in which the intensity and speed of the changes reminded us of what in physics is called a “phase transition”.

But, what kind of phase transition? The theory of phase transitions is a broad field in physics. It is maybe true that most of the results of the theory of phase transitions lie far away from biology; but it is also true that a lot of this theory is becoming more and more relevant in understanding biological phenomena. This was an intriguing a topical problem with several theoretical models of material phase transitions emerging (Petridou and Heisenberg, 2019; Lawson-Keister and Manning, 2021), but rather disappointingly we couldn’t experimentally match these models to our in vivo system. During the poster session of the retreat, I (Bernat, who had just joined Edouard’s group as his first postdoc) was discussing these issues with Nicoletta. Soon after, we came up with the idea that this “phase transition”-like behaviour could be addressed as a network phase transition. A network phase transition is a sudden change of the network properties that is usually associated to smooth changes in the connectivity of the nodes. For example, if one removes connections of a network gradually, we will observe that the net commonly remains more or less stable until it abruptly breaks into many small fragments. In this particular example, the exact point of the connectivity that triggers the fragmentation is a critical point of a phase transition between unconnected and connected network regimes, called “percolation”.  Network phase transitions play a relevant role in understanding ecosystems, epidemic spreading or material properties, among many other systems.  In the past I had been working on several problems involving network phase transitions, and the idea of explaining phenomena in embryo development with this framework was as much exciting as unexpected, and marked the start of a beautiful collaboration between biologists and physicists. We combined approaches originating from both biology and physics to address a key problem of embryo development, in a truly two-way collaboration trying to overcome the artificial borders between fields of knowledge.

Back to IST, we started frantically analyzing embryo tissues as if they were a network made of cells (nodes) and links (the cell-cell contacts) between nodes (Fig. 1A). At a first sight, the results were not really encouraging: The networks of cell-cell contacts were not that different before and after the fluidization event. What could be reported was just a small, smooth drop in the average number of contacts per cell coinciding with the fluidization point (Fig. 1A). However, when dealing with phase transitions, one has to be careful not to neglect the relevance of small changes in some parameters of the system: close to the critical point (the point where the system changes its phase), any tiny fluctuation can result in an abrupt, macroscopic change. For example: if we leave a glass of water in the fridge at 0.1^oC, it will remain forever liquid; if we drop the temperature an almost imperceptible 0.2^oC, therefore putting the fridge at -0.1^oC, the water in the glass will sooner or later freeze, which is a radically different state than the one we had when we were at 0.1^oC. And somehow this was similar to what was happening in the embryo: the tiny decay in the number of contacts per cell was precisely crossing a critical point: the critical point of rigidity. That is, in a network with a lower number of average contacts per cell, the system as a whole remains floppy, and one can deform it with almost no effort. Beyond the rigidity threshold, no independent movements of the cells are possible without applying a force over the system. In particular, a rigid cluster of nodes (called Giant Rigid Cluster – GRC) abruptly emerges, almost spanning the whole network, and thereby opposing resistance to any deformation (Fig. 1B). The critical point in rigidity (also called the “rigidity percolation threshold” or “isostatic point”) is found when the number of average contacts per cell is 4 (which corresponds to the 2/3 of the maximum potential connectivity of a network, that is, 6, if one considers a complete packing made of a large number of hexagonal-like cells) (Fig. 1B). Strikingly, this is one of the older, if not the oldest, prediction of a critical point, as the result goes down to Maxwell (Maxwell, 1870), who solved the problem in the middle of the XIX century.

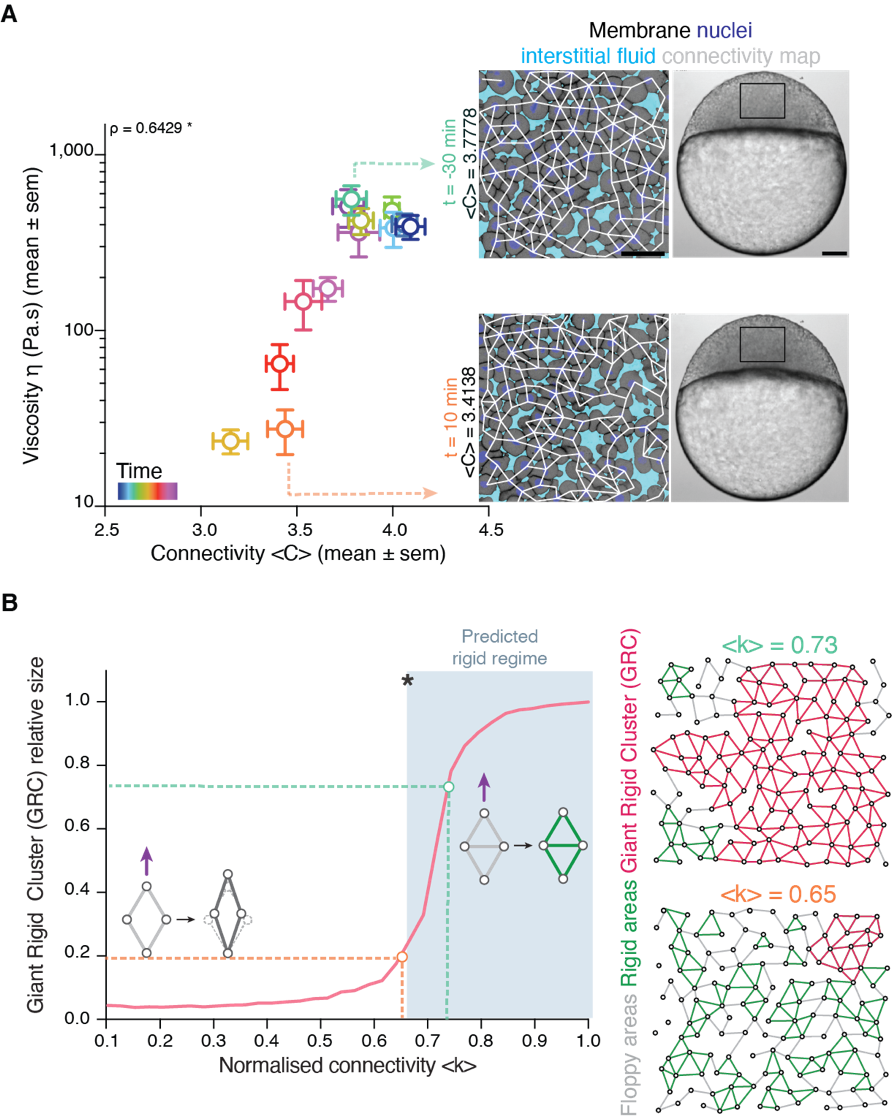
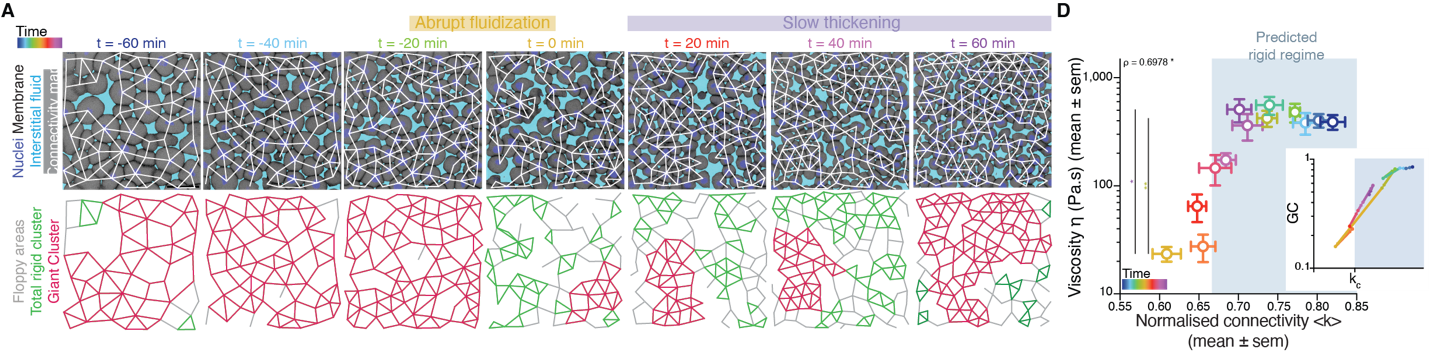
It turned out that, indeed, fluidization occurred at the moment where the average number of contacts per cell went below the critical point of 2/3 of the maximum cell connectivity of the tissue (Fig. 2). But there was more: after that, the number of average contacts per cell increased very slowly, but crossing the critical point again to start “thickening” and recovering its viscosity/rigidity (Fig. 2). The incredible correspondence of experiments to the theory of network rigidity percolation and viscosity by solely one simple criterion, cell connectivity, triggered one of these paradoxical moments in science where the excitement of the discovery is immediately followed by an uncomfortable feeling of uncertainty due to the overwhelming number of new questions that the discovery implies.

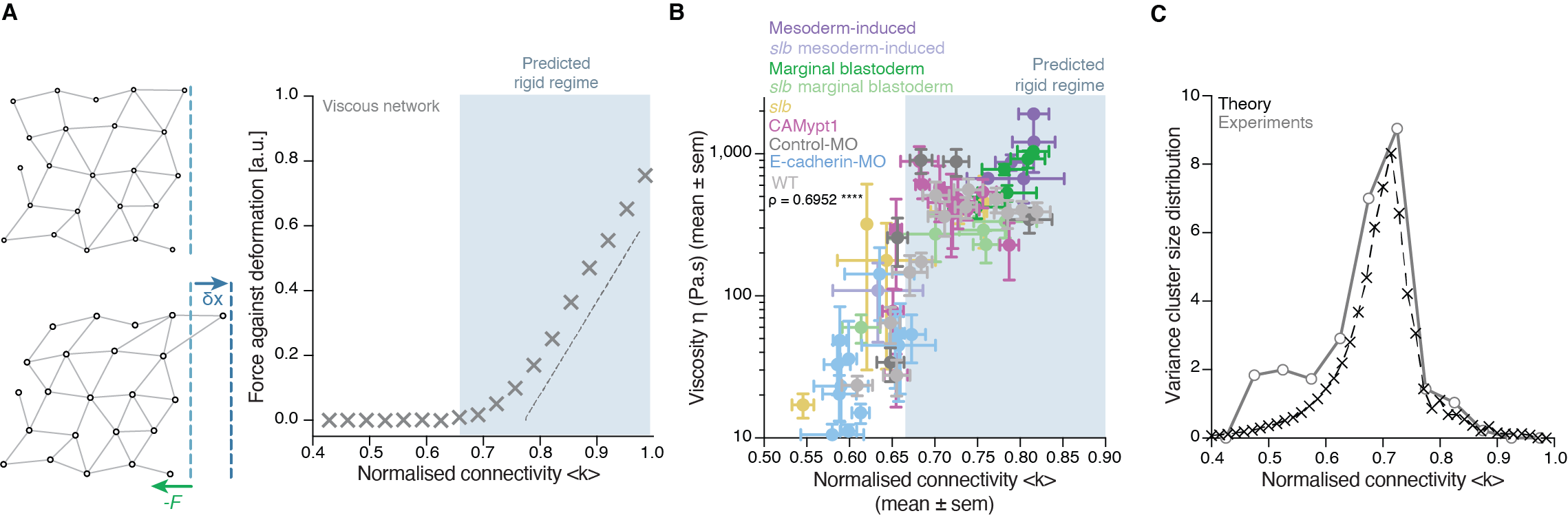
There was, first, a theoretical problem: We were measuring tissue viscosity, but the theory is about topological properties of the networks. Intuitively, they seem related, but we wanted a rigorous connection, as it is the key tie between theory —and its predictions— and experiments —with its observations. This turned out to be an interesting problem of bridging description scales: on the one side, we have a microscopic property, namely, the number of connections per cell, and on the other side, we had a macroscopic property, namely, the viscosity, hypothetically emerging from the microscopic structure. With the help of computer simulations and theoretical arguments, we could prove that, indeed, the critical point in connectivity for rigidity transitions triggers a qualitative shift in the behaviour of viscous networks. From almost negligible force response values in the region where the network is floppy, a sudden, steady increase is observed when passing the rigidity percolation point (Fig. 3A). In addition, we wanted to test the generality of our approach. How reliable is connectivity as a control parameter for predicting the different viscosity regimes of the tissues? We experimentally measured cell connectivity, tissue rigidity (GRC size) and tissue viscosity in numerous experimental conditions. For example, we examined this in embryonic tissues with differences in cell-cell adhesion, contractility, cell fate, geometry, genetic backgrounds: remarkably, using only the connectivity value, we could reproducibly predict the rigidity regime of the tissues (Fig. 3B).

Once we had established a theoretical and experimental connection between connectivity rigidity and tissue viscosity, we wanted to know if indeed what we observed in the embryos corresponded to a genuine phase transition. This was a great challenge for us, and when we started sharing our results with the scientific community, many sceptical questions followed. What class of a PT is this? How can it be a true PT in such a small living system? Such criticism is indeed necessary when merging fields especially when there are no similar examples or guidelines on the right way to do it! To prove a phase transition in physics for example, it requires to find the traces of a singularity or divergence in a macroscopic observable in terms of a control parameter that, in turn, increases smoothly. In addition, in a high order phase transition —as it is the case of rigidity percolation—, one expects to observe characteristic phenomena, like power-law statistical patterns of the diverging observable. Having a large amount of experimental data allowed us to perform reliable statistics and unambiguously detect such patterns. In particular, in rigidity phase transitions a singularity/divergence is expected to occur at the critical point of the phase transition which corresponds to the variance in the size of the rigid clusters other than the GRC. We observed a clear diverging trend in the experimental data and well-defined traces of a power-law distribution in the size of rigid clusters (Fig. 3C), with exponents compatible with the theory. These findings suggested that the embryo is operating very close to a surprisingly well-defined critical point of phase transition or, in other words, that the embryo is at criticality.

Many puzzling questions were constantly opening up: Can we engineer the system to fine-tune its material properties based on its network representation? Can we transform this simple but “static” representation of rigidity into a dynamic model taking into consideration the time-scales of cell and tissue viscoelasticity? The finding that the tissue is poised at criticality also gave a twist to our research, because we realised that we not only have a framework to predict the tissue material state but we can start exploring questions regarding robustness and stability of the system. To address this question within the proper environment, we met many times enjoying the bitter and intense taste of the expresso at Coffee Pirates —our favourite coffee shop in Vienna. And we always came to the same, fundamental question: What is the benefit of a living system being poised at criticality? A system at criticality can change its state with almost no energy investment, thus criticality could be an effective strategy in this developmental stage. However, this comes with a cost: a system at criticality is highly unstable, and this is not what we experimentally observe. For example, the rigidity phase transition occurs only once in the embryo at the onset of its morphogenesis. How is the embryo precisely operating between rigid and floppy regimes when positioned so close to the critical point? Our results so far suggest that synchrony in the cell division may play a fundamental role. Cell connectivity in the early embryo is dominantly regulated by cell division, where cell-cell contacts between neighbouring cells disassemble during mitosis and reassemble during interphase. We also found evidences of a counterintuitive but interesting relation between spatio-temporal randomness in cell division patterns and temporally precise and spatially uniform changes in tissue structural and material properties (Petridou et al., 2021).

Well, this was the moment when we knew that we could not answer all the questions –at least, not within our postdoc period! We never thought that this interdisciplinary scientific retreat could lead to such a fruitful collaboration, especially since it took us a long time to find a common communication language between physics and biology. We spent hours for example discussing what rigidity means in physics or what adhesion means in biology, going back to basic textbooks! We are very grateful to both CP and Edouard for supporting this challenging project, and, now, equipped with this full package of unanswered questions, we are both looking forward to address experimentally and theoretically how tissue rigidity and criticality orchestrate embryo development in our very recently starting groups at EMBL Heidelberg (Nicoletta) and University of Graz (Bernat), respectively.

References

Lawson-Keister, E., and Manning, M.L. (2021). Jamming and arrest of cell motion in biological tissues. arXiv. doi: arXiv:2102.11255.

Maxwell, J.C. (1870). I.—On Reciprocal Figures, Frames, and Diagrams of Forces. Transactions of the Royal Society of Edinburgh 26(1), 1-40. doi: 10.1017/S0080456800026351.

Petridou, N.I., Corominas-Murtra, B., Heisenberg, C.-P., and Hannezo, E. (2021). Rigidity percolation uncovers a structural basis for embryonic tissue phase transitions. Cell 184(7), 1914-1928.e1919. doi: https://doi.org/10.1016/j.cell.2021.02.017.

Petridou, N.I., Grigolon, S., Salbreux, G., Hannezo, E., and Heisenberg, C.P. (2019). Fluidization-mediated tissue spreading by mitotic cell rounding and non-canonical Wnt signalling. Nat Cell Biol 21(2), 169-178. doi: 10.1038/s41556-018-0247-4.

Petridou, N.I., and Heisenberg, C.P. (2019). Tissue rheology in embryonic organization. EMBO J 38(20), e102497. doi: 10.15252/embj.2019102497.

There are dozens more ‘behind the paper’ stories featuring the highs and lows and serendipities of research on our dedicated page. Does your paper have a story behind it? We’d love to hear it.

(6 votes)

Loading...