Allometry in a Simple Cell Network

A post by Jasmin Imran Alsous, on work done in collaboration with Paul Villoutreix and Alexander M. Berezhkovskii in the Shvartsman lab.

I started working on Drosophila egg chambers from the day I joined the Shvartsman lab. Egg chambers are small clusters of cells that eventually develop into mature oocytes in the abdomen of the female fruit fly. Perhaps not surprisingly, because the development of gametes, oocytes (or sperm), within such clusters is a conserved feature from insects to mammals, there is much to learn from probing their development within these simpler organisms. As I was taught how to dissect out the egg chambers and take images of the ovarioles – these are strings of egg chambers lined in a chronologically ordered array (Figure 1B) – I knew that regardless of what my project(s) turned out to be, it would have to involve these clusters: their structure was simple and images of the fluorescently labeled egg chambers were really beautiful. Both features meant I would not quickly tire of collecting data and could explain my research to non-biologists and non-scientists in general with little difficulty.

Interesting Phenomena in Developing Egg Chambers

Most questions we asked in the lab about how these egg chambers develop arose naturally from simply observing these structure as they formed and grew. First, the egg chamber is a cluster of exactly 16 germline cells that are enveloped by an epithelium. These 16 cells arise from a single founder cell that undergoes four synchronous and incomplete divisions: the cells remain connected through bridges, called ring canals, that allow for intercellular transport and communication (Figure 1A). One of these cells becomes the oocyte, and the other 15 develop into endoreplicating nurse cells that synthesize RNA, proteins, and organelles; these are then transported to the oocyte. Because the divisions are stereotypic, each of the 16 cells is uniquely identifiable, so one of the earliest questions we asked was whether the cells are packed or spatially arranged in a stereotypic manner also (this became the subject of another project). Second, as the egg chamber develops and grows, it does so non-uniformly, i.e. the tremendous gain in volume, by roughly 4 orders of magnitude, is distributed unequally among the 16 cells (Figure 1B). Interestingly, previous studies dating back to the late 50s had made note of this, and I was amazed at how much was known about the egg chamber already – its structure, its cell type composition, the specialized functionalities of the oocyte and nurse cells, its various stages of development –  and frankly, a lot of the questions I was interested in were either posed in one way or another in these initial studies or inspired by them. However, without a proper sample size and comprehensive quantification, which would have been impossible without today’s imaging technologies, it was unclear whether there was a pattern to this nonuniformity, and by which mechanism it arose. The project was then to answer these two questions, and it eventually culminated in our recent Current Biology paper, “Collective Growth in a Small Cell Network”.

Differential Growth: Examples & Mechanisms

This phenomenon, of parts in growing objects growing at different rates, is not an unfamiliar one. Perhaps some of the clearest examples of that are the disproportionately large deer or elk antlers and fiddler crab claws (Figure 2A, B). These structures are evidently growing at faster rates than the animal’s other body parts. Another example closer to home is a human baby during postnatal development: born with a relatively large head and small limbs, the toddler develops into an adult with a proportionally smaller head and larger limbs (Figure 2C).

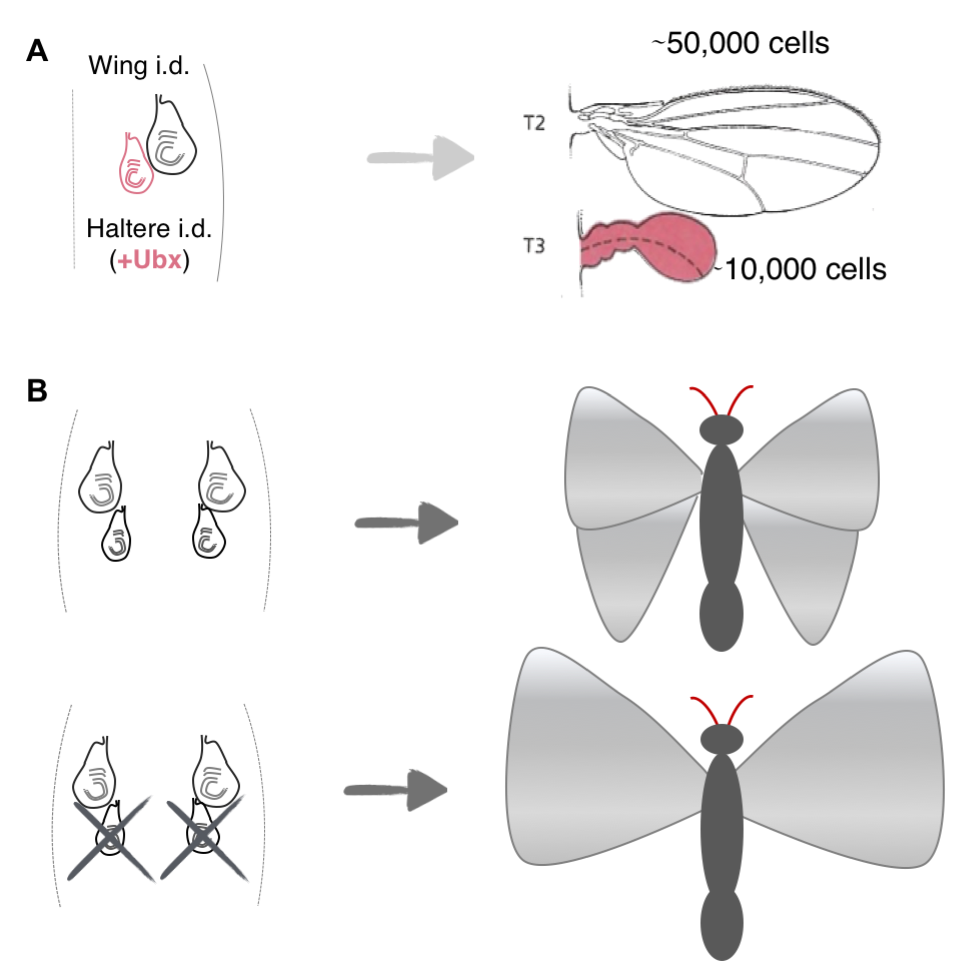
How such spatiotemporal patterns arise in growing organisms have fascinated researchers since Huxley and Thompson’s times [5, 6], and recently, studies have come up with potential mechanisms to explain these emergent collective growth patterns in model systems. For example, studies have shown that the size discrepancy between the Drosophila wings and halteres, which are a second and smaller pair of appendages (~fivefold fewer cells) used for balance and steering, can be explained by intrinsic differences, i.e. expression of the gene ultrabithorax (ubx) in the imaginal discs in the larva that give rise to the halteres, but not the ones that give rise to the wings (Figure 3A) [7]. Another elegant study showed that the difference in size between the fore and hind wings on butterflies, P. coenia, can be explained by competition for resources among the growing wing appendages (Figure 3, top). This was best exemplified by experiments that surgically removed the patch of cells that give rise to the hind wings: in such butterflies, the researchers noted a compensatory increase in the size of the forewings (Figure 3, bottom) [8]. Although these model systems are considerably simpler than whole organisms, they are still relatively complex: both systems comprise thousands of cells and the developing structures are not independent, but are parts of a whole.

A Correlation & An Observation

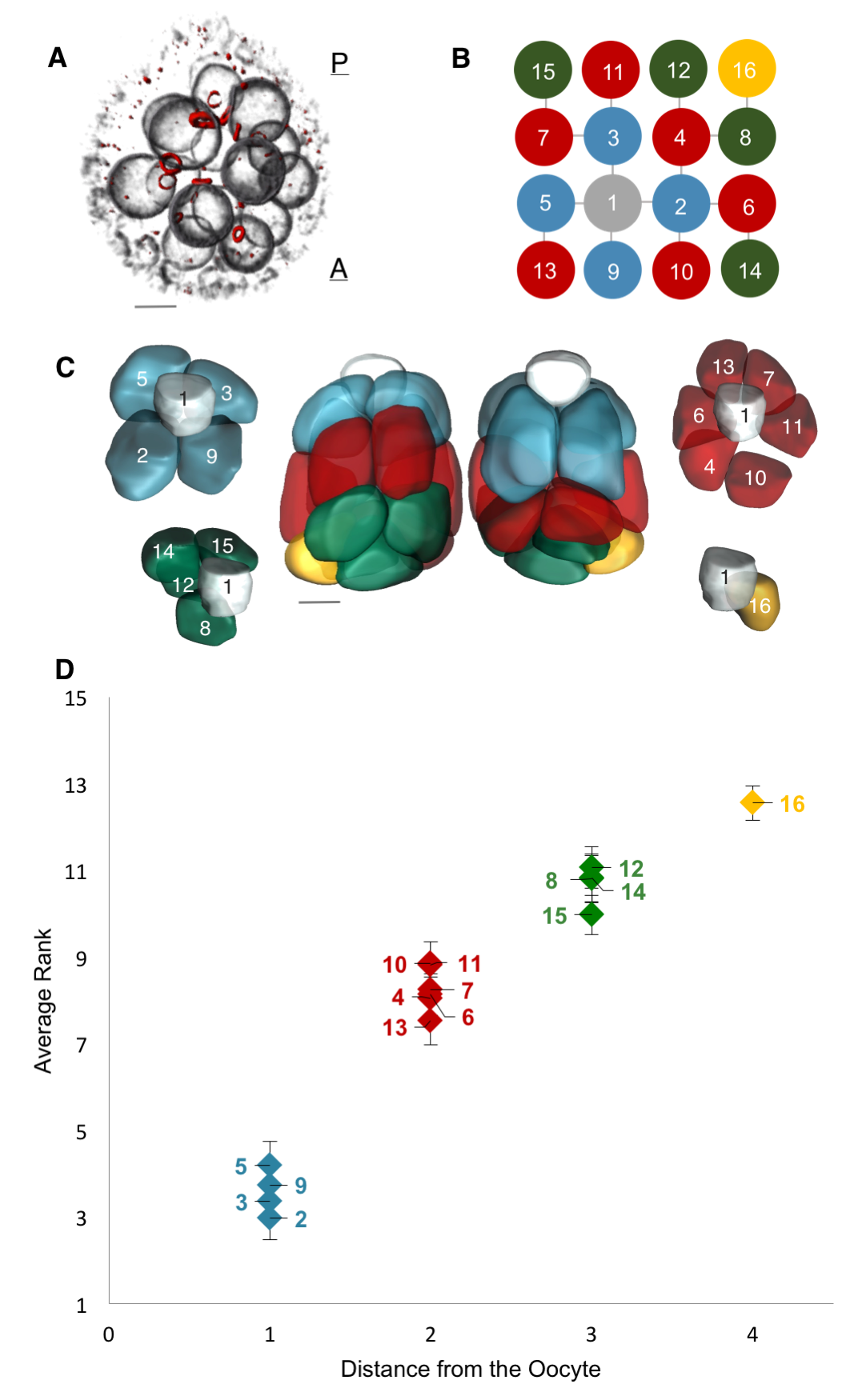
Motivated by these examples, we set out to quantify the nonuniformity of cell sizes in the growing egg chamber, and if possible, to describe and mechanistically explain the emergent pattern. To that end, we collected a large number of 3D confocal images of egg chambers that were immunostained to reveal their cell membranes, nuclei and ring canals. Using the stereotypic structure of the cell lineage tree, and starting with the oocyte, labeled as cell 1, we identified and annotated each of the 16 cells (Figure 4A, B). Furthermore, using nuclear and membrane volume measurements of reconstructed egg chambers, we had previously found that nuclear and cell volume correlate strongly, so for our subsequent measurements, we used nuclear volume as a proxy for cell volume – a much more easily measurable parameter than cell volumes: obtaining cell volumes required reconstructing the 3D shapes of each cell in the egg chamber, which involved drawing contours that traced the outlines of the cells’ membranes – a painstakingly slow process because the cells are irregularly shaped and thus far the process has not been automated. These reconstructions also revealed that the nurse cells are spatially organized into layers dictated by the number of ring canals separating any given nurse cell from the oocyte: arranged from posterior (closest) to anterior (furthest) of the oocyte, the numbers of nurse cells that the layers contain are 4, 6, 4, and 1 (Figure 4C).

A Pattern of Cell Sizes

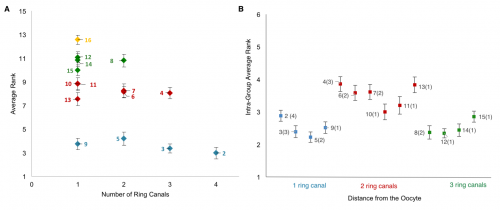
Collecting the data was a two-step process. First, we uniquely identified and labeled each of the cells in each collected 3D image of an egg chamber. Second, we collected nuclear volume measurements for each of those cells. To normalize for variations in growth among different egg chambers, we then ranked each nurse cell within each egg chamber by its nuclear volume. This gave us a vector of 15 rank entries, labeled 1–15, with 1 being largest and 15 smallest, and allowed us to calculate an average rank for each cell across all egg chambers. Once we had that data, it was unclear how to proceed or what correlations to look for: cell size as a function of ring canal number? Or cell size as a function of distance from the oocyte as defined on the lineage tree? Both factors were possible and had been proposed as potentially affecting cell size to some degree. After much plotting, it became clear that distance to the oocyte on the lineage tree was the primary factor affecting cell size (Figure 4D). Namely, we found that cells closer to the oocyte rank more highly and that, naturally, four groups of cell sizes emerge that correlate with their layered spatial organization relative to the oocyte. Interestingly, the number of ring canals each cell has appeared to not have much of an influence on cell size, within or across groups (Figure 5A, B).  More importantly, we found that this pattern of cell sizes emerges from uniform initial conditions, only after the 16 cells are enveloped by the epithelium. These measurements, although critical, were more difficult to make: the divisions that give rise to the cyst take place inside a germarium, which is a structure at the vary anterior tip of the ovariole. This structure contains the stem cell niche and is extremely packed and crowded: identifying separate cysts and labeling the cells from 1-16 required high resolution images in x, y and z, a lot of zooming in and forgoing any sense of urgency.

Origin of This Pattern

Having established the pattern of cell sizes, our next step was to come up with the simplest mathematical model that can both explain our observations and make predictions. This process of developing and writing out the model was perhaps the most exciting, but the most iterative: the model was written and re-written more times than I can remember, mainly because at each iteration, we found that the model could be simplified further. In fact, the final version that appears in the paper is a model that exhibits how differential growth arises already in a 2-cell system, and how groups of cell sizes arise in a 4-cell system; these results are easily generalizable to the 16-cell system and there was little need to write out the equations for all 16 cells in the main body of the paper (these made their cumbersome way to the supplementary material).

We started with a coarse-grained model whose variables corresponded to cell volumes,  which increase according to Monod-like kinetics: proportional to the product of the current cell volume of cell  and a monotonically increasing function of the intracellular concentration of some limiting component (Figure 7B). Intuitively, differences in the cellular concentrations of the limiting factor result in different specific growth rates among the cells. Notably, we were unsure as to what that limiting component was: was it a nutrient, a protein, an organelle? Were there several limiting components? The study alluded to in figure 3B that established that the size discrepancy between the fore and hind wings in the butterfly was due to competition for resources remained “deliberately vague” as to the nature of the shared components, so we felt emboldened to do just the same. Figuring out the nature of that component became an item on the future works agenda.

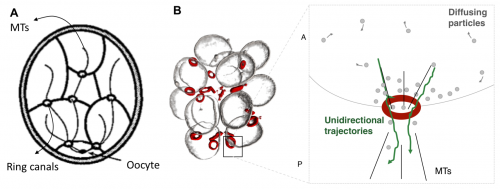
We then postulated that this component is exchanged among the cells and that this exchange is polarized, such that the probability of being transported through a ring canal connecting any two cells is higher in the direction of the more posterior cell, i.e. the cell closer to the oocyte. Here we also defined the parameter v, which quantifies the asymmetry of transport through the ring canals such that when transport is polarized in the posterior direction, v<1.  Notably, this bias in transport across the ring canals is made possible by a polarized network of microtubules that is set up following specification of the oocyte and that extends from the oocyte to the nurse cells through the ring canals, connecting all cells within the germline cyst (Figure 6A) [9, 10]. Furthermore, several particle tracking studies in developing egg chambers showed that particles diffuse randomly in the cytoplasm of the cell, and while particles can diffuse bi-directionally across a ring canal, once at a ring canal, these particles exhibit a posterior bias in their translocation (Figure 6B) [11, 12, 13, 14].

We also assumed that concentrations within the cell cluster equilibrate rapidly and can therefore be considered at steady state on the much longer timescale of growth of the cyst. This assumption was based on the difference between our estimate of the time it takes a diffusing particle to reach a circular window of some radius on the wall of a cell with some volume, and the time scale for growth. The former was estimated to be around 10 minutes; the latter, ~ 3 days. Note that it helped that our advisor and our collaborator (SYS and AMB) had co-authored a paper on the kinetics of escape through a small hole – one of the main results of that paper was an analytical expression for the rate constant of escape, k, in terms of the problem’s parameters: the diffusion constant, D, of the particle, the hole radius, a, and the cavity volume V : k=4Da/V [15].

We then wrote out equations illustrating how the fluxes between any two connected cells balance, and given that the fluxes can be expressed in terms of a rate constant for diffusion multiplied by the cellular concentration of our limiting component, this gave us relationships that related (1) the concentrations between any two anterior and posterior cells separated by either a single ring canal and (2) the intercellular concentration of any anterior cell relative to the oocyte, cell 1. Based on these assumptions alone, the model explained both the observed pattern of differential growth and the emergence of groups in wild type egg chambers. Specifically, when transport is polarized toward the founder cell, i.e. v<1, the 2-cell system gives us differential growth (Figure 7C), and the 4-cell system gives us both differential growth and emergence of (three) groups (Figure 7D). These results were easily generalizable to the 16-cell cyst.

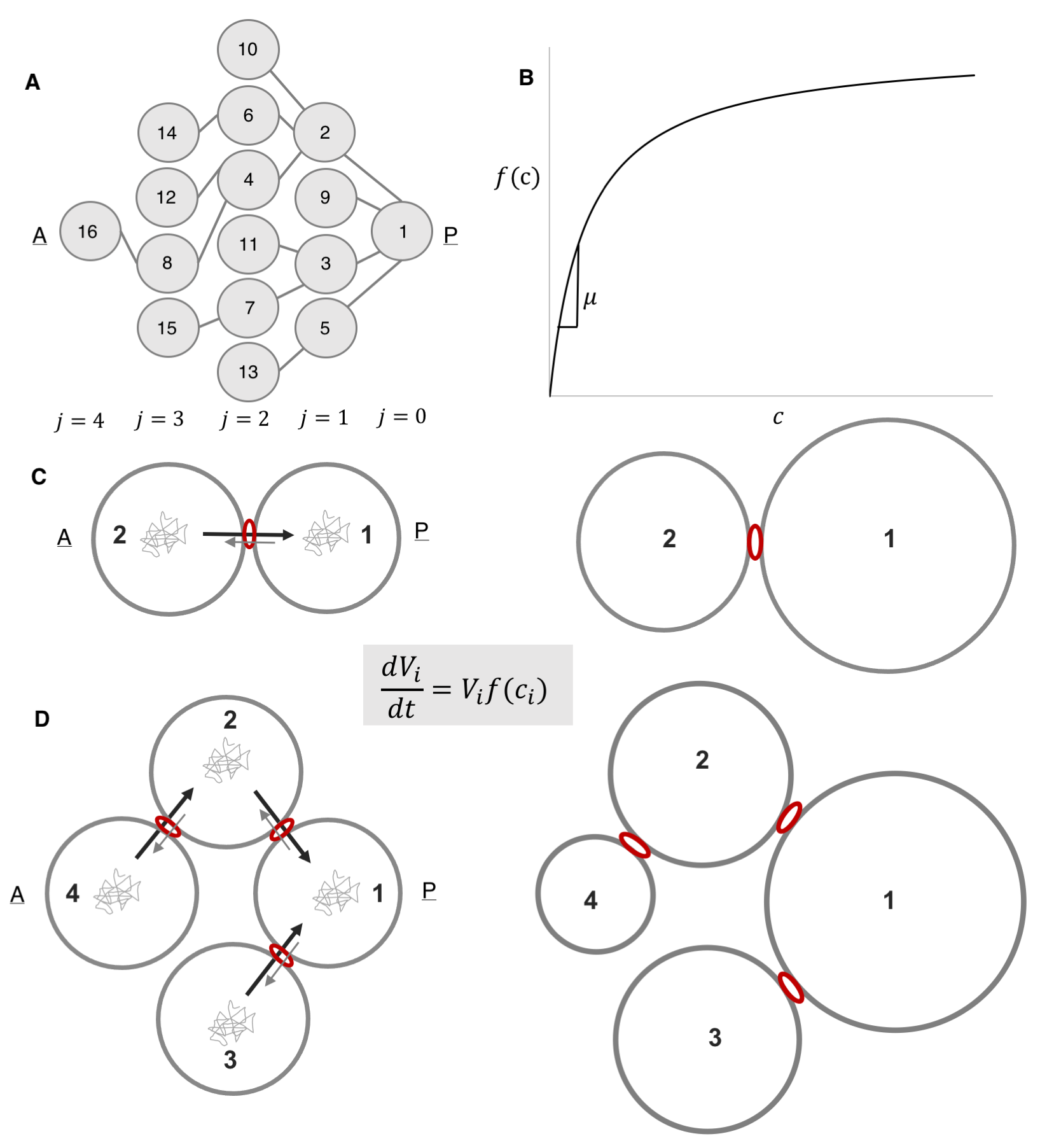
Our model also made a prediction, namely, that in the absence of a polarized transport network and polarized transport (v=1), cells in the growing cluster would be of the same size. We therefore examined mutants that fail to set up a polarized microtubule cytoskeleton for transport. Luckily, there are several such mutants available but we chose egalitarian (egl) in which no oocyte is specified, the formation and maintenance of a polarized microtubule network are disrupted, and all 16 cells develop into polyploid nurse cells [9]. We showed that in such mutants, the group-wise arrangement of cell sizes observed in wild type egg chambers was absent: the average size ranks of cells from virtually all groups overlap. These results suggested that the relative absence of both differential growth and emergence of groups of cell sizes is attributable to the absence of a polarized transport within the cluster.

Allometric scaling

We were pretty happy with the model: it was simple, had few assumptions and could explain our observations in both wild type and mutant egg chambers. But we wondered whether we had extracted all of what the model had to offer, and we had not. By making an additional assumption, namely that we were in the linear regime of the proposed growth law (shown in Figure 7B), we could extract a quantitative relationship between the volumes of cells belonging to different layers in the cell network in terms of already-defined problem parameters.

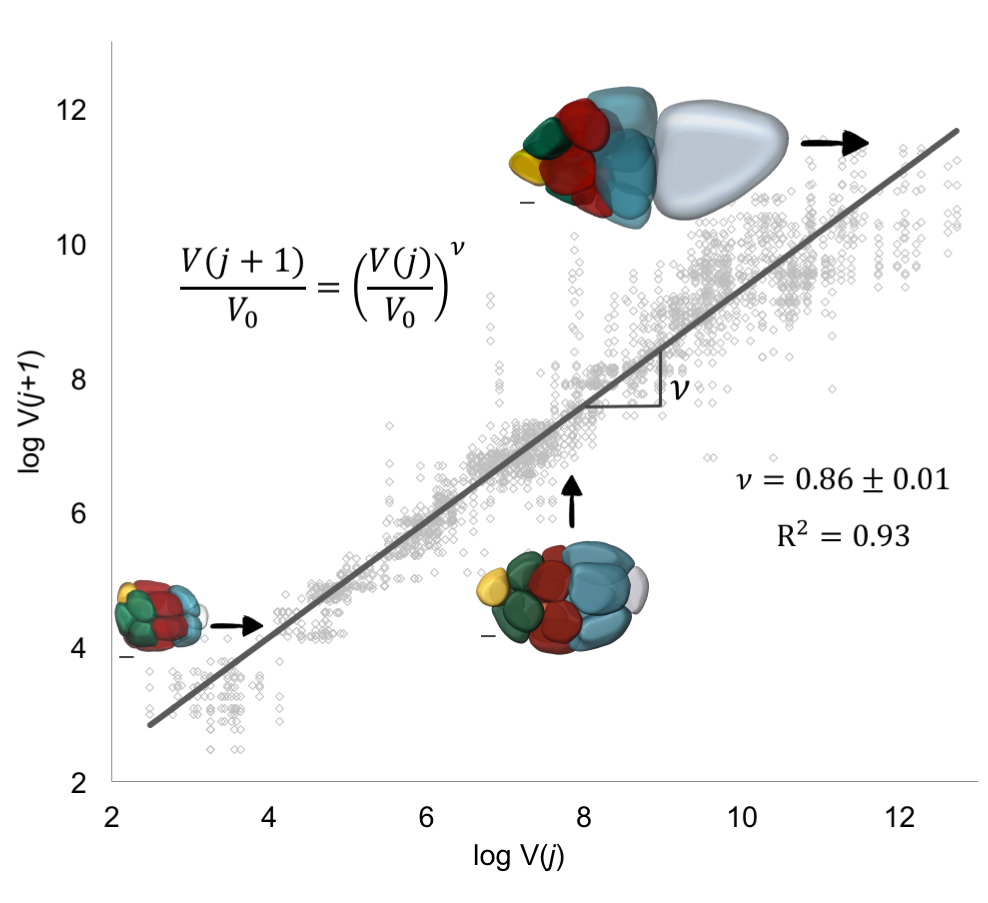
This result now predicted a specific quantitative pattern for a thus far qualitative observation, namely, that the pattern of decreasing cell sizes with distance from the oocyte at any moment in time can be quantified with an allometric-type relationship. The only parameter here was v, which linked a process occurring at the molecular scale, transport of an intracellular limiting component, to an observable phenotype, cell size. To estimate v, took the natural logarithm of both sides of the equation in the previous paragraph: the value of v was then given by the slope of the line that best fits through pairs of nuclear volumes of nurse cells from consecutive layers j and j + 1; each egg chamber has 52 such pairs (Figure 8). This lead to v =0.86±0.01. For this value of , which is less than 1, transport is polarized (biased towards the oocyte), and a growing egg chamber will have four groups of nurse cells that exhibit a posterior-to-anterior gradient of decreasing cell sizes, which is consistent with what we observed experimentally.

We were particularly happy with this result because in addition to deriving the quantitative relation between volumes of cells from different layers, we also extracted the parameter characterizing the extent of polarized transport within the cluster, thus linking a subcellular molecular process to an emergent pattern of collective cell growth. It is not often that one can link processes that span different scales in biology, regardless of how phenomenological the starting model is, and being able to come back full circle to Huxley’s allometries is cool.

This paper was perhaps one of the most rewarding project I had been involved in so far – mainly because we finally answered basic questions about growing egg chambers that we had been interested in for quite some time, and because the model that explained our results was relatively simple and could be dissected and understood to the end. Perhaps the biggest challenge in writing up the paper was deciding how to most clearly explain our experimental observations and theoretical results to a broad community of cell, developmental, and quantitative biologists, as well as applied mathematicians: we wanted to avoid writing a cumbersome paper but not at the risk of imprecision. However, having several lab mates, collaborators and, of course, co-authors from various backgrounds who read and re-read the manuscript streamlined that process and ensured that we used the most correct yet simplest terminology, so thanks friends.

References

[1] Imran Alsous, J., Villoutreix, P., Berezhkovskii, A.M., and Shvartsman, S.Y. (2017). Collective growth in a small cell network. Current Biology. doi: dx.doi.org/10.1016/j.cub.2017.07.038.

[2] Australian National University. “Size Doesn’t Matter to Fighting Fiddler Crabs.” ScienceDaily. ScienceDaily, 8 January 2008. <www.sciencedaily.com/releases/2008/01/080101192723.htm>.

[3] “Deer Antler Velvet—What Is It, How Does It Work?” National Geographic, 1, February 2013 <http://news.nationalgeographic.com/news/2013/01/130130-deer-velvet-antler-spray-science-health-football-sports/>.

[4] “Growing up (and out, and sideways, and around)…” Society of Vertebrate Paleontology (SVP), 23, December 2013.  < http://vertpaleo.org/Society-News/Blog/Old-Bones-SVP-s-Blog/December-2013/Growing-up-(and-out,-and-sidways,-and-around).aspx>.

[5] Thompson, D.W. (1917). On Growth and Form (Cambridge University Press).

[6] Huxley, J.S. (1932). Problems of Relative Growth (Methuen).

[7] Crickmore, M.A., and Mann, R.S. (2006). Hox control of organ size by regulation of morphogen production and mobility. Science 313, 63-68.

[8] Nijout, F.A., and Emlen, D.J. (1998). Competition among body parts in the development and evolution of insect morphology. PNAS 95, 3685-3689.

[9] Theurkauf, W.E., Alberts, B.M., Jan, Y.N., and Jongens, T.A. (1993). A central role for microtubules in the differentiation of Drosophila oocytes. Development 118, 1169–1180.

[10] Theurkauf, W.E., Smiley, S., Wong, M.L., and Alberts, B.M. (1992). Reorganization of the cytoskeleton during Drosophila oogenesis: implications for axis specification and intercellular transport. Development 115, 923–936.

[11] Bohrmann, J., and Biber, K. (1994). Cytoskeleton-dependent transport of cytoplasmic particles in previtellogenic to mid-vitellogenic ovarian follicles of Drosophila: time-lapse analysis using video-enhanced contrast microscopy. J. Cell Sci. 107, 849–858.

[12] Nicolas, E., Chenouard, N., Olivo-Marin, J.C., and Guichet, A. (2009). A dual role for actin and microtubule cytoskeleton in the transport of Golgi units from the nurse cells to the oocyte across ring canals. Mol. Biol. Cell 20, 556–568.

[13] Snee, M.J., and Macdonald, P.M. (2004). Live imaging of nuage and polar granules: evidence against a precursor-product relationship and a novel role for Oskar in stabilization of polar granule components. J. Cell Sci. 117, 2109–2120.

[14] Shimada, Y., Burn, K.M., Niwa, R., and Cooley, L. (2011). Reversible response of protein localization and microtubule organization to nutrient stress during Drosophila early oogenesis. Dev. Biol. 355, 250–262.

[15] Grigoriev, I.V., Makhnovskii, Y.A., Berezhkovskii, A.M., and Zitserman, V.Y. (2002). Kinetics of escape through a small hole. J. Chem. Phys. 116, 9574.

(1 votes)

Loading...