A biology-modeling crosstalk to uncover feather pattern evolution

Richard Bailleul, Jonathan Touboul and Marie Manceau

Patterning in question: 60 years of mathematical and biological studies

The coat of Vertebrates displays a stunning diversity of motifs created by the spatial arrangement of appendages and pigments across the skin surface. Strikingly, many have similar periodicity (i.e., number of repetitions within a period of space or time) or orientation along body axes within taxa or species. This reproducibility, key to fitness, is likely shaped by developmental constrains. A long-standing scientific challenge has been to understand the tissue, cell and molecular mechanisms underlying the emergence of natural patterns and to what extent these processes contribute to pattern evolution.

Alan Turing’s milestone 1952 paper “The chemical basis of morphogenesis” (ref 1) conceptualized the principles of pattern formation through self-organization: instabilities within an initially homogeneous surface or volume may cause the spontaneous arrangement of distinct characters in a pattern. The mathematical model Turing described involved two diffusing factors, an activator and a repressor, as well as a catalyst, and since his pioneering work, a plethora of models based on Turing’s theoretical framework have been used to generate a great diversity of patterns that visually resemble those observed in nature through in silico computer simulations (ref 2). Biological validation of mathematical models such as Turing mechanisms is however a difficult task, because a single pattern can often be reproduced by a variety of models that may represent very distinct biological processes. Conversely, a single model can often generate a variety of patterns when its parameters are changed. In addition, models often allow reproducing patterns arising at equilibrium (i.e., stable states) but are not developed to anticipate progressive steps in dynamics of pattern emergence. They thus rarely produce realistic hypotheses on the developmental paths to pattern formation.

Biological studies of animal patterns have identified patterning molecules and cellular events through the use of mutant screens in genetic systems such as fish or mice, or expression analyses of “usual suspect” factors (refs 3, 4). These studies showed that diffusing molecules called morphogens dictate cell fate depending on their local concentration, creating spatial differences and tissue boundaries within developing organs (ref 5). However, interpreting empirical tests has been limited by the difficulty to link a given pattern to prior events occurring in the initially homogeneous tissue devoid of spatial reference, and to date, only a few pattern-forming factors have been identified in vivo. The current culprits for applied mathematicians and developmental biologists are on the one hand, designing mathematical models able to realistically guide biological experimentation of patterning mechanisms and on the other, validating (or contradicting) theoretical predictions through in vivo experiments.

Using natural variation to engage a math-bio dialogue

To engage efficient crosstalk between theoretical and empirical approaches, Richard Bailleul, a PhD student in applied mathematics, joined the laboratories of Jonathan Touboul, which focuses on mathematical modeling of living systems, and of Marie Manceau, which studies developmental processes of pattern formation. Richard took advantage of the highly reproducible, stereotypical arrangement of feather follicles in bird plumage and designed a modeling approach whereby a unified mathematical model is to be confronted not only with final plumage patterns in one bird species, but also with its dynamics of developmental emergence for several groups chosen across the bird phylogeny. Our idea was that by being more restrictive, modeling would be more powerful to design simple empirical tests.

From one-by-one to all at once: a breadth of patterning dynamics

The timely emergence of feather follicles had been previously meticulously described in the domestic chicken: follicles individualize gradually, forming longitudinal rows in a medial-to-lateral “wave” of differentiation. This row-by-row dynamics results in a regular dotted pattern covering the “tract”, which is the area of the skin covered by feathers (ref 6). We performed a comparative spatio-temporal survey by marking feather follicles throughout completion of the dorsal tract (using in situ hybridizations for ß-catenin). In addition to the domestic chicken we used other poultry birds, namely Japanese quails and Common pheasants, collected from local farmers. All three species represent Galloanserae, one of the three major bird groups (ref 7). To represent the second group, Neoaves, we chose the zebra finch, a passerine songbird widely studied for its inherited singing behavior for which we have a breeding colony at the Collège de France, and the emblematic Gentoo penguin whose eggs were collected directly from breeding colonies in the Falkland Islands. Finally, emus (eggs were provided by local breeders) were studied to account for the derived, ancestral group of Paleognathes, which also comprises ostriches or tinamous. Much like penguins – used here for the first time in developmental studies – emus do not fly, which we suspected would provide more sizable variation in plumage patterns and their emergence. Richard’s results demonstrated that this is the case: we observed extensive variation in the final shape and width of the dorsal tract (Figure 1).

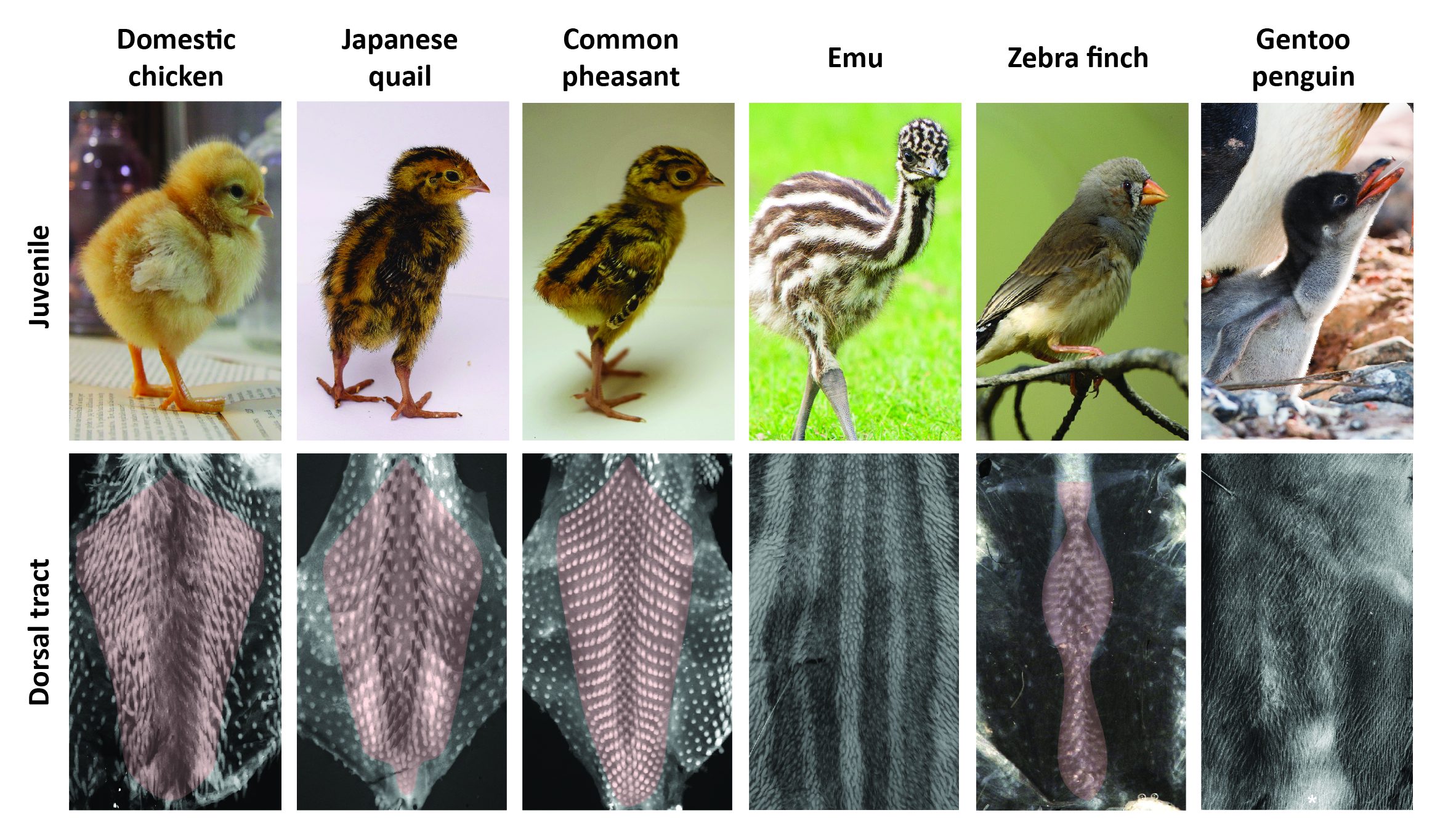
In all poultry birds and the zebra finch, this tract forms in a row-by-row sequence of follicle-forming lines, patterning duration for tract completion being similar despite differences in hatching times. Species vary however in the location and shape of the first-formed, medial-most rows. Emus and penguins sharply contrast with other species: their feather follicles individualize simultaneously and in a comparably shorter developmental window within wide competent areas (Figure 2). Follicle size also varies between species (e.g., much bigger in the quail than in the zebra finch), as well as their local geometrical arrangement (ranging from sparse and irregularly distributed in the emu to a striking, extremely dense and highly symmetrical pattern in the penguin). Variation in patterning dynamics is thus a combination of differences, with not only duration and transitory states of plumage patterning changing substantially between species, but also follicle size, regularity or spacing constituting very diverse attributes. With such imbrication, it was time for math to take the baton.

Initial conditions trigger directional reaction-diffusion, chemotaxis and proliferation

Inspired by the extensive literature that followed Alan Turing’s work – in particular modeling studies of virus spreading and population behavior – we developed a model combining two preeminent processes previously used to explain feather patterning, namely reaction-diffusion equations akin to Turing’s original model and chemotaxis that represents cell movements towards chemical factors (ref 8, 9), with an explicit mathematical term describing cell proliferation as an autonomous logistic function. This term implements growth in systems with resource limitations [Ref 10] and classical theories of diffusion equations with logistic growth are known to develop traveling waves, spreading initial perturbations through directional nearest-neighbor contagion. Simulations of the resulting unified model reproduced final pattern differences as well as species-specific patterning dynamics, without forcing onto an extrinsic wave as was previously done (Ref 11), but only by applying measured axial initial conditions corresponding to the position of first-formed follicles on simulation frames of species-specific sizes (Figure 2).

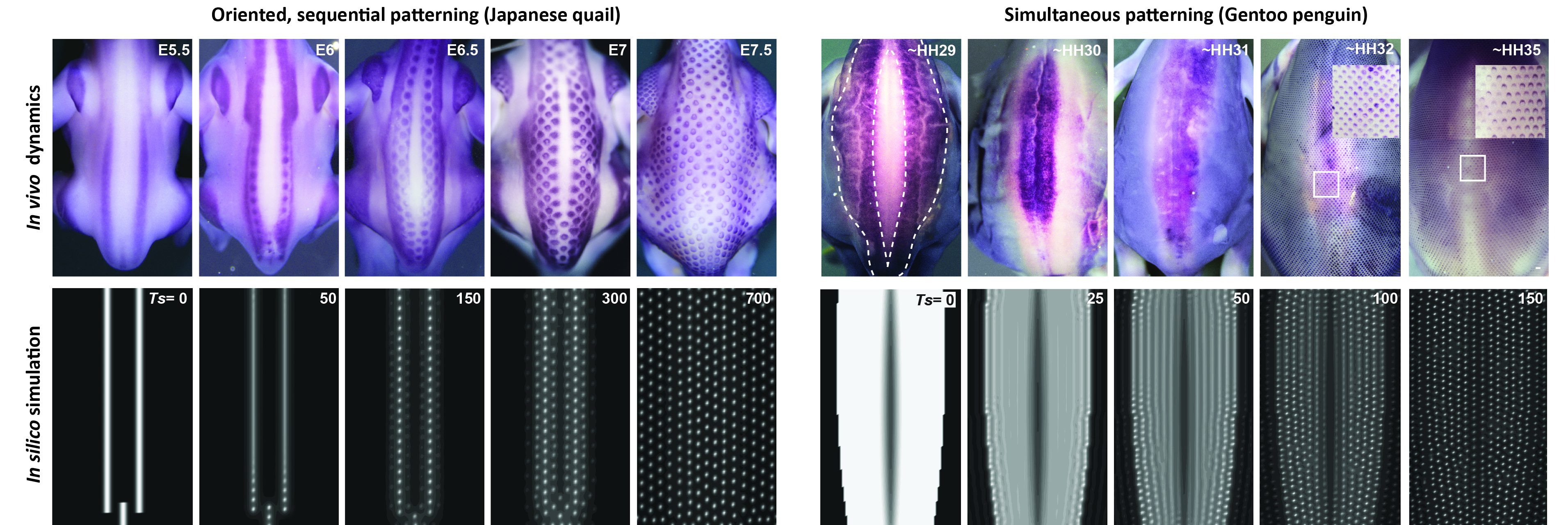
We played with parameter values, the geometry and orientation of initial conditions, or proliferation rates, and formulated two major predictions:

– Initial conditions trigger the follicle wave sequence and control its species-specific sequence (i.e., in a row-by-row dynamics when initial conditions are spatially restricted and sharp enough, or simultaneously otherwise)

– The proliferation rate of the logistic source controls the duration of the patterning process by governing the timely lateral propagation of an increase in cell density.

Equipped with these predictions, Richard went back to the bench.

Logistic cell proliferation dictates patterning duration

We chose to investigate the relevance of model-based predictions by analyzing dynamics of cell proliferation throughout tract differentiation in the Japanese quail. We confirmed the existence of a travelling front of increased cell density that progressively provides follicle-forming competence to longitudinal domains as it propagates laterally. Was it acting in a logistic-like fashion? We thoroughly analyzed confocal images of BrdU-stained developing skins and showed that the ratio of proliferative cells, linearly decreasing with respect to cell density, ceases when the skin tissue attains a certain carrying capacity (i.e., a cell density threshold; Figure 3). Cell proliferation thus occurred exactly according to predictions of a logistic growth term. This result represents a unique in vivo validation of this widely used mathematical equation. Drug treatments on skin explants inhibiting proliferation without altering the carrying capacity of the skin demonstrated that proliferation rate governs pattern duration, also supporting the predictions of the model.

On feather pattern evolution… and what about penguins?

This study established a fruitful dialogue between theory, numerical simulations and in vivo experimentation and thereby showed that if a self-organizing feather follicle individualization recipe is conserved among birds, initial conditions in the naïve skin system differ. This variation produces changes in the directionality and sequence of developmental paths to pattern establishment. Competence to form feather follicles travels through the lateral transfer of increased cell proliferation, at a rate controlling a certain lapse of pattern duration, eventually completing tract patterning in a species-specific time.

As we tracked various developmental paths, we can propose that in emus and penguins, the converging loss of featherless area in the dorsum, and potentially, of flight ability, may be due to an absence of sequential patterning. Whether sequentiality has been lost during evolution remains to be studied, although it is likely the case in the penguin, which is part of otherwise flying Neoaves birds. Moreover, we suggest that the loss of flight is likely unrelated to local pattern geometry and regularity, attributes that differ in emus and penguins with the latter displaying an extremely dense, squared geometrical arrangement of its follicles. Despite implementing realistic sizes of computational frames to our simulations, our mathematical framework does not explain some singularities observed in the penguin, suggesting that additional patterning mechanisms are at stake in these emblematic birds; this is the promise of further back and forth between the computer and the bench.

Check out our paper in PLOS Biology here.

References

1. Turing AM. The chemical basis of morphogenesis. Phil. Trans. Roy. Soc. Lond. 237:37–72 (1952).

2. Hiscock TW, Megason SG. Mathematically guided approaches to distinguish models of periodic patterning. Development. 142:409 (2015).

3. Asai R, Taguchi E, Kume Y, Saito M, Kondo S. Zebrafish leopard gene as a component of the putative reaction-diffusion system. Mech Dev. 89, 87-92 (1999).

4. M. Manceau, V. S. Domingues, R. Mallarino, H. E. Hoekstra, The developmental role of Agouti in color pattern evolution. Science 331, 1062–1065 (2011).

5. Nüsslein-Volhard, C.; Wieschaus, E. “Mutations affecting segment number and polarity in Drosophila“. Nature. 287 (5785): 795–801 (1980).

6. Sengel, P. Morphogenesis of the Skin. Cambridge University Press (1975).

7. Prum, R. O., Berv, J. S., Dornburg, A., Field, D. J., Townsend, J. P., Moriarty Lemmon, E. & Lemmon, A. R. A comprehensive phylogeny of birds (Aves) using targeted next-generation DNA sequencing. Nature 534, 7–8 (2016).

8. Lin CM, Jiang TX, Baker RE, Maini PK, Widelitz RB, Chuong CM. Spots and stripes: Pleomorphic patterning of stem cells via p-ERK-dependent cell-chemotaxis shown by feather morphogenesis and mathematical simulation. Dev Biol 334, 369-382 (2009).

9. Mou, C. et al. Cryptic Patterning of Avian Skin Confers a Developmental Facility for Loss of Neck Feathering. PLOS Biology 9, e1001028 (2011).

10. Verhulst PF. Notice sur la loi que la population poursuit dans son accroissement. Correspondance mathématique de physique. 10:113–121 (1838).

11. Michon, F., Forest, L., Collomb, E., Demongeot, J. & Dhouailly, D. BMP2 and BMP7 play antagonistic roles in feather induction. Development 135, 2797-2805 (2008).

(5 votes)

Loading...