Forces maintain order between cells
Posted by boudaoud, on 30 April 2019
Written by Antoine Fruleux and Arezki Boudaoud
As Lewis Wolpert put it (Wolpert, PLoS Biology 2010), if you extend your two arms, you will likely find that they match in length by better than 0.2%, though they do not seem to directly communicate during their development and growth. Similarly, flowers in an individual plant are likely to be almost identical in size and shape. Such precision, or robustness, in organ size might seem trivial when conceptualizing observations as reflecting a ‘developmental program’ with series of well-defined steps and ‘decisions’, but it is less so when thinking of the myriad of cells that form an organ and that divide and grow asynchronously (Figure 1). This raises the question of how organs and organisms reach well-defined sizes and forms, in the face of considerable spatial and temporal fluctuations of cell growth and deformation during morphogenesis (Hong et al. 2018, Uyttewaal et al. 2012, Kierzkowski et al. 2012, Hipfner et al. 2004).

Figure 1. Cell growth is heterogeneous in space and time. Example of a sepal (green leaf-like organ that protects a flower before it opens) from the model plant Arabidopsis thaliana. The color scale corresponds to growth rates (high in red, low in blue).
This question might find a very simple answer. As an organ grows larger and larger, an individual cell has less and less influence on overall size and shape of the organ; accordingly, precision of organ size would increase with the number of its cells. This is somehow like taking many independent measurements of an experimental parameter, the precision of the mean value of the parameter increases with the number of measurements, or, equivalently, the standard error of the mean (SEM) decreases with the number of measurements according to the law of large numbers. In an organ, if cells expanded randomly and independently from each other, then organ growth rate, which combines growth of all cells, would become increasingly precise as the number of cells increases (Hong et al. 2018). Nevertheless, this scenario cannot be fully true because cells communicate with each other and, therefore, are not necessarily independent. This led us to investigate how growth fluctuates according to the size of the region of interest, from cell to organ, so as to understand how precision of organ size can be achieved (Fruleux & Boudaoud, 2019). Interestingly, an independent and complementary study obtained results that are similar to ours (Damavandi & Lubensky, 2019).
A key question is whether there are mechanisms that enhance robustness of organ shape. If growth fluctuates between cells, those growing relatively fast will tend to push their neighbors, generating forces within the tissues. More generally, any tissue with heterogeneous growth builds up internal forces (internal stress) due to conflicts between cells or groups of cells. Such internal forces might be instructive: They could be sensed and used by cells to regulate their growth (Shraiman, 2005). This can be pictured by thinking of a group of blindfolded persons, each holding the hands of two neighbors, all involved in a round dance. Each dancer moves at its own natural pace and so pace fluctuates from dancer to dancer; as a consequence each dancer feels forces from the hands of the neighbors. Can the dancers use information provided by these forces to circle at the same speed?
Cells within a tissue can sense and respond to forces. It was first hypothesized that proliferation is affected by such forces, with cells under mechanical compression or tension reducing or increasing their division rates, respectively (Shraiman, 2005), which has received indirect and direct support in developing fruit fly and zebrafish (LeGoff et al., 2013; Campinho et al. 2013; Mao et al., 2013; Pan et al., 2016). The cytoskeleton may also respond to forces: actomyosin cables are reinforced by mechanical tension in the wing imaginal disk of Drosophila (LeGoff et al., 2013; Duda et al., 2017). The synthesis of the extracellular matrix (ECM) might also be modulated in response to mechanical signals. In plant cells, growth is driven by the cell’s inner pressure and restrained by the cell wall (the equivalent of the ECM) that encloses cells. The deposition of cellulose fibers, the main load-bearing component of the plant cell wall, depends on wall tension (Hamant et al. 2008, Hervieux et al., 2017), likely leading to reinforcing the cell wall in the direction of maximal tension (Sampathkumar et al., 2014). We aimed to incorporate all these responses to mechanical signals in a unifying framework, so as to be able to reach conclusions that may be relevant to robustness of morphogenesis in many developmental systems.
We described a tissue as a two-dimensional (2D) absract continuous medium, so as to make the calculations tractable and the conclusions general; a 2D model captures all main processes at play (notably directional processes such as those related to cytoskeleton), while a continuous model enables to disregard the details of cell arrangements and describe them at a supracellular level. We assumed the medium to be viscous, which accounts for the long-term relaxation and remodeling of cell junctions, cytoskeleton, ECM, or cell wall. We assumed the medium to be anisotropic; anisotropy is quantified with a mathematical object known as nematic tensor, which has been extensively used to measure fibril orientation and degree of orientation in cells and tissues (Boudaoud et al., 2014). We describe in the model the dynamics of density (density of cells, of cytoskeleton, of ECM, or of cell wall) and nematic tensor, that vary in time and space due to tissue expansion and deformation and to synthesis; for instance, ECM density decreases if tissue expands without synthesis, increases if cells exocytose ECM components, while ECM fibers align passively if the tissue is stretched in one direction.
Up to this point, all assumptions are rather straightforward. Our key additional assumption is that synthesis is modulated according to mechanical stress, reflecting the evidence mentioned above: density is modulated (positively or negatively) in response to level of mechanical stress and anisotropy is modulated (positively or negatively) in response to directional mechanical stress; the corresponding response parameters (which may be positive or negative) are the main parameters of our model. Positive response to stress levels describes putative increase in ECM / cell wall synthesis, and subsequent reduction in expansion, in response to tensional stress; negative response to stress levels describes reduction in proliferation due to compression. Positive response to directional stress corresponds to cytoskeleton / cellulose fibers reinforcement under tension; negative respond to directional stress corresponds to cell intercalation under directional stretching. Accordingly, the sign of the response (positive or negative) allows us to account for biological diversity in mechanical responses.




Figure 2. Response to a localized perturbation.Snapshots of the predicted dynamics following a perturbation of tissue density in the form of a disk at time t0. The density is color-coded (white corresponds to no deviation from average density and dark red to large deviations). Tissue anisotropy is indicated by the small lines: the stiffest tissue direction corresponds to line orientation and the degree of anisotropy to line length.
We first examined tissue dynamics following a perturbation in tissue density of a small disk-shaped region (Figure 2), which could correspond to a transient depolymerization of cytoskeleton or a transient reduction in ECM / cell wall synthesis The model predicts the expansion of this region due to tissue growth and the relaxation of density to its average value due to tissue response to mechanical stress; anisotropy orients circumferentially around the perturbed region, like in wound healing. We then considered the effects of a stochastic component to synthesis, reflecting temporal fluctuations of cellular dynamics. The model predicts that cells (more rigorously regions as the model is continuous) are correlated to each other at long distances (Figure 3): Cells do not grow independently (although they synthesize materials independently) and growth fluctuations in one cell remain correlated with growth fluctuations in a cell far apart. Long-range correlations are characterized by an exponent indicating how fluctuations of an element of the tissue scale with its size (Figure 3). Thus individual cells may have a stronger impact on organs size than if they were fully independent.
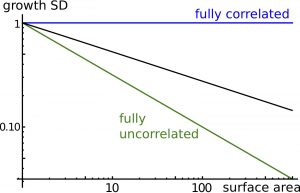
Figure 3. Long-range correlations. Cell-to-cell correlations quantify the degree of spatial coordination between cell fluctuations. The plot shows relative fluctuations in areal expansion of the tissue (growth SD) as a function of size of the region of interest (surface area). If cells wall fully correlated, fluctuations in areal expansion would not depend on size (exponent 0, blue line) and if cells wall fully uncorrelated, fluctuations in areal size would quickly decrease with size (exponent -0.5, green line). In general, the model predicts an intermediate behavior (with exponent ranging between -0.5 and 0, dark line), known as long-range correlations.
Finally, we examined the precision of organ shape and size. Positive response to mechanical stress levels (tissue reinforcement in response to tension) makes organ size less precise than with negative response (tissue softening in response to tension). Interestingly, increasing response to directional stress has a non-intuitive effect on organ precision (Figure 4): first the precision of organ size is enhanced, but then precision reaches a minimum, and then it increases for higher response levels. Thus, the model predicts an optimal response to directional mechanical stress for robustness of organ shape and size (Figure 4). This can be qualitatively understood by getting back to the dance picture. The round dance could be broken if the blindfolded dancers respond too weakly or too strongly to the forces they perceive from their neighbors; accordingly, an optimal response to forces would ensure a harmonious dance.
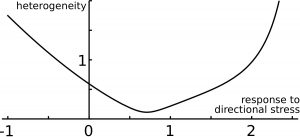
Figure 4.Precision of size and shape. The predicted ‘error’ on organ size (heterogeneity) is shown as a function of the level of response to directional mechanical stress, and features an optimal response level.
Long-range correlations of growth fluctuations are a crucial prediction of our analysis since it is strongly related to how cellular fluctuations impact robustness of morphogenesis. We therefore believe that correlations need to be measured at many scales in different experimental systems, in various genetic backgrounds, and in absence and presence of transient genetic or chemical perturbations. This would enable to disentangle the contributions of cell proliferation, cytoskeleton, ECM, and cell wall to the control of robustness. In addition, we speculate that long-range correlations could be involved in absolute size control; additional work would be required to investigate how this could occur. Finally, we note that we focused here on precision and robustness of morphogenesis, starting from the examples of bilateral symmetry in animals and flowers in plants; but this does not always need to be the case. For instance, plant leaves and roots are phenotypically highly plastic to adapt to environmental constraints. Tumor expansion and metastasis are likely favored by heterogeneous morphogenesis. Altogether, our work sheds light on the importance of considering fluctuations in understanding developmental processes.
References
Boudaoud, A., Burian, A., Borowska-Wykręt, D., Uyttewaal, M., Wrzalik, R., Kwiatkowska, D., & Hamant, O. (2014). FibrilTool, an ImageJ plug-in to quantify fibrillar structures in raw microscopy images. Nature protocols, 9(2), 457. https://www.ncbi.nlm.nih.gov/pubmed/24481272
Campinho, P., Behrndt, M., Ranft, J., Risler, T., Minc, N., & Heisenberg, C. P. (2013). Tension-oriented cell divisions limit anisotropic tissue tension in epithelial spreading during zebrafish epiboly. Nature cell biology, 15(12), 1405. https://www.ncbi.nlm.nih.gov/pubmed/24212092
Damavandi, O. K., & Lubensky, D. K. (2019). Statistics of noisy growth with mechanical feedback in elastic tissues. Proceedings of the National Academy of Sciences, 116(12), 5350-5355. https://www.ncbi.nlm.nih.gov/pubmed/30819899
Duda, M., Kirkland, N. J., Khalilgharibi, N., Tozluoglu, M., Yuen, A. C., Carpi, N., … & Mao, Y. (2019). Polarization of myosin II refines tissue material properties to buffer mechanical stress. Developmental cell, 48(2), 245-260. https://www.ncbi.nlm.nih.gov/pubmed/30695698
Fruleux, A., & Boudaoud, A. (2019). Modulation of tissue growth heterogeneity by responses to mechanical stress. Proceedings of the National Academy of Sciences, 116(6), 1940-1945. https://www.ncbi.nlm.nih.gov/pubmed/30674660
Hamant, O., Heisler, M. G., Jönsson, H., Krupinski, P., Uyttewaal, M., Bokov, P., … & Couder, Y. (2008). Developmental patterning by mechanical signals in Arabidopsis. science,322(5908), 1650-1655. https://www.ncbi.nlm.nih.gov/pubmed/19074340
Hervieux, N., Tsugawa, S., Fruleux, A., Dumond, M., Routier-Kierzkowska, A. L., Komatsuzaki, T., … & Hamant, O. (2017). Mechanical shielding of rapidly growing cells buffers growth heterogeneity and contributes to organ shape reproducibility. Current Biology, 27(22), 3468-3479. https://www.ncbi.nlm.nih.gov/pubmed/29129534
Hong, L., Dumond, M., Zhu, M., Tsugawa, S., Li, C. B., Boudaoud, A., … & Roeder, A. H. (2018). Heterogeneity and robustness in plant morphogenesis: from cells to organs. Annual review of plant biology, 69, 469-495. https://www.ncbi.nlm.nih.gov/pubmed/29505739
Hipfner, D. R., & Cohen, S. M. (2004). Connecting proliferation and apoptosis in development and disease. Nature Reviews Molecular Cell Biology, 5(10), 805. https://www.ncbi.nlm.nih.gov/pubmed/15459661
Kierzkowski, D., Nakayama, N., Routier-Kierzkowska, A. L., Weber, A., Bayer, E., Schorderet, M., … & Smith, R. S. (2012). Elastic domains regulate growth and organogenesis in the plant shoot apical meristem. Science, 335(6072), 1096-1099. https://www.ncbi.nlm.nih.gov/pubmed/22383847
LeGoff, L., Rouault, H., & Lecuit, T. (2013). A global pattern of mechanical stress polarizes cell divisions and cell shape in the growing Drosophila wing disc. Development,140(19), 4051-4059. https://www.ncbi.nlm.nih.gov/pubmed/24046320
Mao, Y., Tournier, A. L., Hoppe, A., Kester, L., Thompson, B. J., & Tapon, N. (2013). Differential proliferation rates generate patterns of mechanical tension that orient tissue growth. The EMBO journal, 32(21), 2790-2803. https://www.ncbi.nlm.nih.gov/pubmed/24022370
Pan, Y., Heemskerk, I., Ibar, C., Shraiman, B. I., & Irvine, K. D. (2016). Differential growth triggers mechanical feedback that elevates Hippo signaling. Proceedings of the National Academy of Sciences, 113(45), E6974-E6983. https://www.ncbi.nlm.nih.gov/pubmed/27791172
Sampathkumar, A., Krupinski, P., Wightman, R., Milani, P., Berquand, A., Boudaoud, A., … & Meyerowitz, E. M. (2014). Subcellular and supracellular mechanical stress prescribes cytoskeleton behavior in Arabidopsis cotyledon pavement cells. Elife, 3, e01967. https://www.ncbi.nlm.nih.gov/pubmed/24740969
Shraiman, B. I. (2005). Mechanical feedback as a possible regulator of tissue growth. Proceedings of the National Academy of Sciences, 102(9), 3318-3323. https://www.ncbi.nlm.nih.gov/pubmed/15728365
Uyttewaal, M., Burian, A., Alim, K., Landrein, B., Borowska-Wykręt, D., Dedieu, A., … & Kwiatkowska, D. (2012). Mechanical stress acts via katanin to amplify differences in growth rate between adjacent cells in Arabidopsis. Cell, 149(2), 439-451. https://www.ncbi.nlm.nih.gov/pubmed/22500806
Wolpert, L. (2010). Arms and the man: the problem of symmetric growth. PLoS biology, 8(9), e1000477. https://www.ncbi.nlm.nih.gov/pubmed/20838659


 (5 votes)
(5 votes)