The toilet paper model
Posted by Scutoids, on 3 August 2018
In LM Escudero´s group, we like developmental biology, mathematical biology and computational biology. We try to be imaginative and get inspiration from simple things… such as a toilet paper roll. Using this tool (and some computers), we claim that we have described a novel geometrical shape… You will be wondering… how do you do that??? You are going to find here: the story behind the discovery of “scutoids”.
First, you need a multidisciplinary group distributed between two buildings: “the wet lab”, with flies and their epithelial tissues, at Institute of Biomedicine of Seville, IBiS (Fig. 1); and the “computer lab” with… well… with a bit of everything (it does not fit in a simple picture… so, see Video 1) at the Faculty of Biology of University of Seville. It is ideal if the two buildings are separated by 1 km, so you can exercise everyday walking between the two labs to interact with the members of each branch.

Fig. 1. A. Tagua (at right, masterful segmenter and drosophilist) and C. Gordillo looking for more scutoids in the fly lab.
Video 1. The computational lab (that is wet if you open the tap) showing P. Gómez-Gálvez and P. Vicente-Munuera, the two first authors, working hard and listening good music.
Very important! You need also an office where both computational and Drosophila worlds can fit together (Fig. 2).

Fig. 2. Very trendy office. Please note the a/c controller, essential if you are based in Seville.
Then, you need a problem to think about while you are walking between the two labs… As animals develop, the initial simple planar epithelia of embryos must be sculpted into complex three-dimensional tissues. These cells pack together tightly. To accommodate the curving that occurs during embryonic development, it has been assumed that epithelial cells adopt either columnar or bottle-like shapes.
We thought that a very logic way to approach the problem of how curved epithelia pack in 3D was to design a computer model with the shape of a toilet paper roll (Fig. 3). The results we saw were weird. Our model predicted that, as the curvature of the tissue increases, columns and bottle-shapes were not the only forms that cells may developed. To our surprise, the discovered geometric solid didn’t even have a name in math! We were happy. Really happy. One does not normally have the opportunity to name a shape. We chose the name scutoid.

Fig. 3. The toilet paper: reality versus model.
The undescribed shape was characterised by having at least a vertex in the lateral surface (Fig. 4). This vertex confers an interesting property to the scutoid: when cells adopt this shape, they can have different neighbours in the upper and bottom surfaces (apical and basal in biology). This is exclusive of scutoids and cannot be done with the “prism”, “trunk” (frusta) or “prismatoid” shapes.
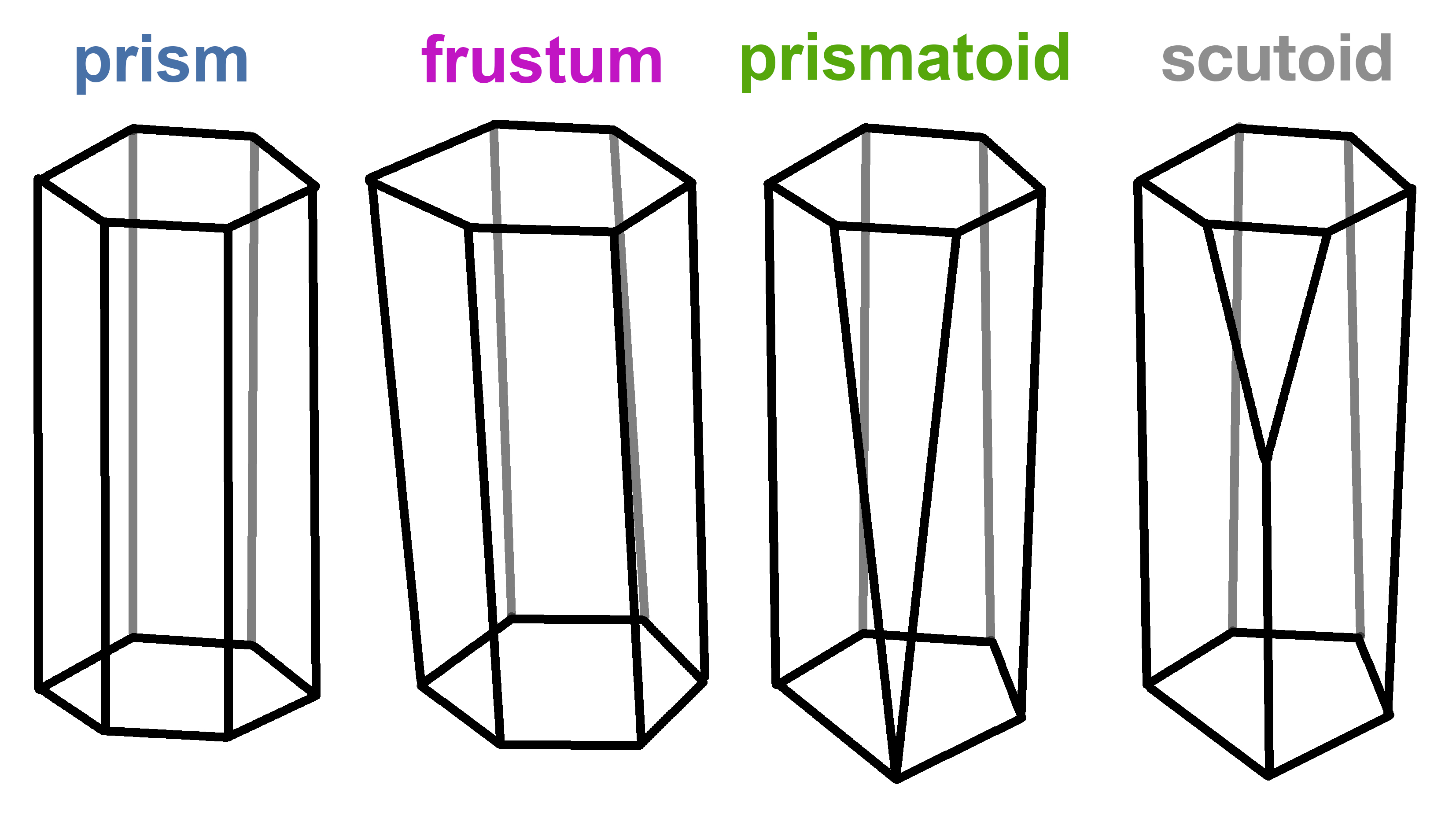
Fig. 4. The brotherhood of the cellular geometry: evolution from prisms to the undescribed scutoid geometrical shapes.
All this was amazing… but we needed help to completely understand the problem. We needed lots of collaborators (we are 16 authors), starting with Dr Grima and Dr Márquez, real mathematicians that helped us with the formal aspects of the toilet paper model.
To verify the model’s predictions, the group investigated the three-dimensional packing of different tissues in different animals. The experimental data, using Drosophila salivary glands, confirmed that epithelial cells adopted shapes and three-dimensional packing motifs similar to the ones predicted by the computational model. This important validation required more collaborators: Dr Sotillos and Dr Martín-Bermudo groups (CABD, CSIC/JA/UPO, Seville) and Dr Cavodeassi (St. George’s University of London) all with biological background but working in other types of epithelia.
And then, the biophysics. We joined efforts with the lab of Dr Javier Buceta (Lehigh University), to study the role of scutoids in tissue architecture from a mechanical point of view. We argue that the scutoids stabilise the three-dimensional packing and make it energetically efficient. Our conclusion was that we have uncovered nature’s solution to achieving efficient epithelial bending. This was really cool… but not so much as the summary that Dr Buceta has prepared for you if you do not have time to read the whole paper… this is art and science in a single sheet (Fig. 5, click to see at full resolution).
Thanks for reading!!!
If you need more information, you can check our paper: Scutoids are a geometrical solution to three-dimensional packing of epithelia. Gómez-Gálvez P, Vicente-Munuera P, Tagua A, Forja C, Castro AM, Letrán M, Valencia-Expósito A, Grima C, Bermúdez-Gallardo M, Serrano-Pérez-Higueras Ó, Cavodeassi F, Sotillos S, Martín-Bermudo MD, Márquez A, Buceta J, Escudero LM. Nat Commun. 2018 Jul 27;9(1):2960. doi: 10.1038/s41467-018-05376-1.
Here you have the link.



 (7 votes)
(7 votes)
Congratulations on being mentioned on the Late Show with Stephen Colbert! Must make that 1 km walk totally worth it :D