The people behind the papers – Ross Carter, Yara Sánchez-Corrales, Verônica Grieneisen & Athanasius (Stan) Marée

Pavement cells in plant leaves were identified as a puzzle which deviated  from normal cell shape rules by D’Arcy Thompson in his classic text On Growth and Form. Now modern approaches allow researchers to revisit these problems and try to uncover the rules that govern pavement cell topology during leaf development. This week we feature a paper – published in the special issue of Development celebrating the centenary of On Growth and Form‘s publication – that uses live-imaging and modelling to understand the development of pavement cell topology. Co-first authors Ross Carter and Yara Sánchez-Corrales, and PIs Verônica Grieneisen and Athanasius (Stan) Marée, told us more.

Stan, can you give us your scientific biography and the main questions your lab is trying to answer?

AM Despite enjoying mathematics and being a computer “nerd” during high school, I initiated my academic trail studying Biology at the Utrecht University, the Netherlands – as I was, and am, most fascinated in how life processes. After performing experimental work on neural vision in cats, I realised I really was a theoretical biologist. I modelled the full life-cycle of Dictyostelium discoideum, and found the driving question for the rest of my carrier:  how do individual cells operate collectively to form complex structures. In a broad sense, my lab uses multi-level modelling of morphogenesis to answer this, in both plants and animal systems. We find that it is particularly important to contrast independently evolved multi-cellular systems, and to work closely to experimental data. So my lab brings together intra- and intercellular communication, cell mechanics and motility, networks and cell differentiation, and cell shape and cell topology, to eventually understand how tissues, organs and even whole organisms are shaped.

And Verônica, what about you?

VG My origins lie in Physics, which I studied in my birth country, Brazil. There I got extremely interested in Statistical Mechanics and Complex Systems. Before I realised it, I ended up meeting Paulien Hogeweg – founder of Bioinformatics – with whom I did my PhD, in Theoretical Biology. This work was done in close collaboration with Ben Scheres, who introduced me to the hidden beauties of Arabidopsis thaliana. I never looked back. Plants are a great system to investigate problems of pattern formation and emerging morphogenesis, with an added twist: their interaction with the environment, for example foraging, light competition, etc, has to go through growth, which means that their development is extremely plastic. My lab seeks to understand this, and we have found that a key integrator of the necessary information processes stems from cell and tissue polarity. My lab explores issues of cell and tissue polarity (for example the development of the Pavement cell), by combining experiments and imaging with computer simulations (like the work here), and even taking an morphogenetic engineering standpoint.

Ross and Yara, how did you come to be involved in the project?

YSC I did my PhD at the John Innes Centre (JIC) under the supervision of Veronica Grieneisen and Enrico Coen. My research focused on investigating the role of different cellular processes during tissue growth. It was very important to obtain data on the dynamics of cell shape morphogenesis and divisions, so I devoted a considerable amount of my PhD to optimize live-imaging of the developing leaf for long time periods. In parallel, I had to find ways to extract meaningful information from the time-lapse data. I had a chance to develop some tools to analyse cell shape dynamics and was extremely lucky to get access to other computational tools that were being developed by Matthew Hartley and Stan’s lab, and were crucial for this research. We started addressing the problem of topology by the end of my PhD, but the real push for this work came when Ross joined Veronica and Stan’s labs. By then, I had already moved to Cambridge.

RC I’ve been interested in leaf development since the start of my PhD in 2010 and after joining Veronica and Stan’s groups in 2015 was given access to an amazing dataset collected by Yara. These time-lapse images collected throughout leaf development really allowed us to address some unanswered questions. Inspired by some work by Matthew Gibson (Nature 2006) we investigated whether our data fit with the topological models they were proposing. When we found that it didn’t we began to investigate why, and the fact that we heard about this special issue allowed us to frame the research to unanswered questions in ‘On Growth and Form’, specifically the puzzling shapes of leaf pavement cells.

Your paper features in Development’s Special Issue celebrating the centenary of D’Arcy Thompson’s On Growth and Form. How has Thompson’s work influenced your thinking about plant development, and what makes his ideas relevant today?

AM D’Arcy Thompson has influenced my work in more than one way, which is remarkable. One of the premises of his book is that living matter also needs to abide to physical laws, and he shows how surface tension can be regarded as an important driving force. While he provided proofs by analogies, my lab follows this inspiration, using the Cellular Potts Model, among others showing how formally it can be linked to Cell Surface Mechanics in Biology. Secondly, D’Arcy is sometimes criticised by not taking genes into account. In fact, he clearly mentions that differential activity of growth and mechanics is what is shaping the organism (and not the gene itself), and I think he is completely correct about that. The control information cannot simply be explained by a gene being expressed. My lab also takes this point of view, but linking gene regulatory networks – which we analyse through dynamical systems theory –  to the actual growth and development of the tissue. And thirdly, it was D’Arcy which first showed in quantitative detail the similarities in the cellular distributions among neighbouring cells between biological and physical cellular matter. This publication is an example of what kind of unexpected discoveries we can make when following such an analysis by modern means.

VG  I believe that D’Arcy Thompson was visionary in the way he was making links crossing disciplines, and bringing together very diverse species to show commonalities. I sometimes like to imagine how delighted he would be if he could see the approaches we currently have in the lab to actually follow up some of his insights: tracking of cell dynamics, computational models to test ideas, and powerful shape analysis methods. However, I am also constantly reminded of something he points out throughout his book: that observing something very elaborate and complex does not imply that the mechanism itself is complex to the same level. His message is something that guides my labs research constantly: are we capturing the phenomenon correctly, are we missing something essential, is the data distracted us?

And finally, D’Arcy Thompson’s ability to look across species to bring forth relevant relations is something we lost, as each field dived into its particular model system. With more advanced molecular methods, however, we will hopefully gain the ability again to zoom out, without losing depth. I am excited about these promising possibilities.

In fact, my first contact with the book was when I was an undergrad physics student, when I came across a worn-out, dog-eared copy of his book in the library. I immediately was totally fascinated by it, actually causing me to enter the field of biophysics during my masters. (Please note that I also gave a radio 4 interview on how he has inspired me.)

Why do pavement cells pose a particular problem or puzzle for those interested in cell topology?

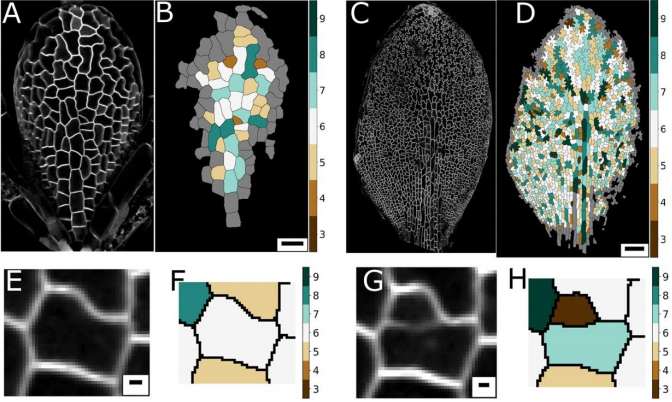
AM & VG Historically, and based on physics, topology is often seen as emerging from cellular interactions that effectively capture surface-minimizing processes, together with mathematical constraints of tessellating structures. Pavement cells, with their extreme perimeter to area ratios, clearly do not fit in a picture of energy minimisation. Moreover, throughout the tissue and over time there are huge differences in cell area. Together this should give rise to a very broad topology distribution which moreover should change dramatically over time. The reality, however, turns out to be totally different.

YSC The peculiar morphology of these cells and the fact that they cannot exchange neighbours made them a very intriguing model to test whether they could follow the typical topological pattern found in animal cells. I was very “puzzled” by these cells, I wrote a blogpost about them some time ago for Botany One.

RC A lot of previous work on cellular topologies has been done either on animal tissues, where membrane tension dominates or on tissues with regular cellular shapes. Pavement cells have neither of these properties and allowed us to address the question of whether these processes are important. These cells start off as quite regular oblong shaped cells and gain their characteristic jigsaw puzzle shape once they have differentiated. We were interested in whether the topological fingerprints we see were due to the shape of the cells or how they ‘choose’ to divide.

Can you give us the key results of the paper in a paragraph?

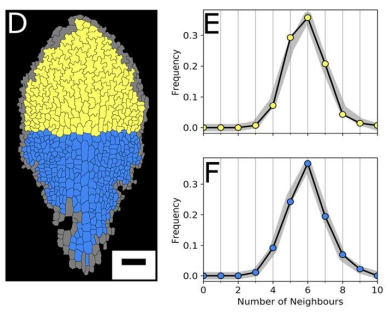
AM & VG Our results surprisingly showed that PC topology establishes very early on during development, independent on the rounds of cell division and pre-established before the cells acquire complex shapes and large differences in cell sizes. At the same time, we found that the topology is unique, compared to other species or other Arabidopsis tissues. This could only be explained if cell divisions are actually (directly or indirectly, this remains an open, exciting question) taking the topological organisation into account when they divide. So, the cell wall is carefully placed while “counting” its neighbours. We show this both through modelling the division dynamics and comparing it to the real date of more than 50,000 cells, and through further confirming it by tracking the division events themselves. The observation that tissues “care” about their topology offers a whole new search image to think about tissue development and functionality.

YSC We used live-imaging and modelling to study cell topology in a developing plant tissue.  Surprisingly, the leaf epidermis has a unique topological signature that is independent of stage, position along the leaf and cell shape. We tested different hypothesis and found that neighbourhood relationships in the leaf can be recapitulated by implementing simple rules of cell division. Therefore, we concluded that the topology in the leaf is mostly determined by cell division rather than cell-surface mechanics.

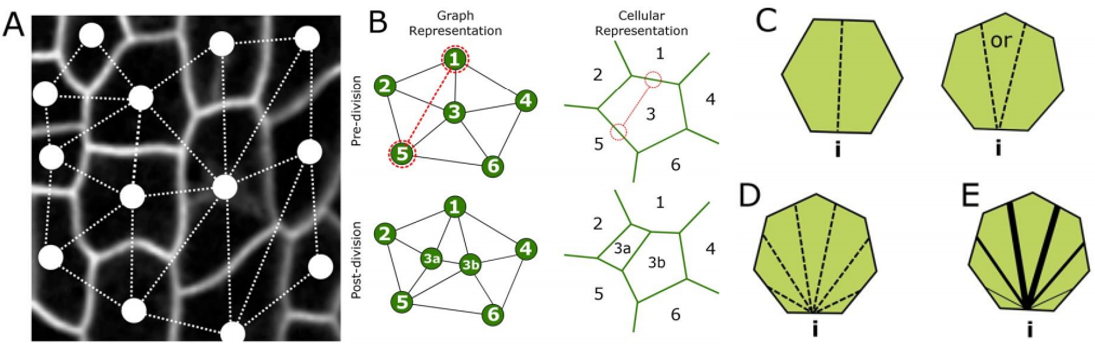
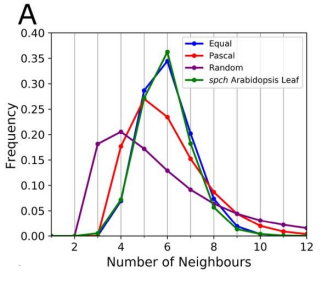
RC We developed an abstract topological model of cell division to test whether or not this can recapitulate the topological distributions we see in the developing leaf. Surprisingly we found that a simple division model, which splits a cell’s neighbourhood in half, was able to reproduce the topological distributions we see with remarkable accuracy. We hope that this will encourage people to think about topology when looking at cell division as apposed to cell geometry and mechanics.

Do you think your model’s insights are restricted to pavement cells (or similar ‘misfits’), or can it explain other topologies in plant and animal tissues?

AM & VG We think that the particular way tightly coordinated division decisions strictly preserve the pavement cells’ unique neighbourhood distribution, might be quite specific for this system, likely linked to the particular cell shapes the PCs later acquire. However, from our study as well as other studies, it starts to emerge that complex mechanisms might operate in order to establish the right topology. The lack of surface tension-driven processes and the large variation in cell sizes allowed us to lay this bare much more clearly for this system, but topology control itself might be much more generic. Future collaborations and interdisciplinary studies will be needed to shed more light on both the how and the why.

YSC I think the insights gained with our set of graph models would help contrasting topological profiles in other epidermal tissues.

RC The rules we implemented in our model give the shallowest and broadest topological distributions (neighbour distributions) of any model we have seen, both the geometrical and the markov models. We did compare our results to some previously published data, and found that there were some similarities, for example with Anthurium, but this data is quite limited. The benefits of the modelling framework we’ve introduced here are that it’s relatively easy to add new topological division rules and, as long as you have a segmented image of a tissue, to compare it with cellular topologies of other organisms, both animal and plant.

If cell division history can explain the observed topology of pavement cells, do you have any idea about the molecular rules of the topology? (One might propose spindle regulators/cell division kinases etc. to have a role)

AM & VG A friend and collaborator of ours, Alan Champneys, proposed to us the idea of a “tent model”, in which neighbours can be “counted” by assessing the location of the triple junctions, similarly to how a tent is positioned by pegs. Molecular processes could thus arise due to cytoskeletal components. Alternatively, it is also possible that substances diffuse amongst cells, for example through plasmodesmata, reaching certain distributions only if the topology is correct, biasing division otherwise.

YSC Our Equal split neighbour division rule fits very well the observed topological distribution in the leaf. There are two possibilities to explain this in biological terms: 1) cells are assessing their number of neighbours after division using an unknown molecular mechanism or 2) our observations are a side effect of other underlying division and growth mechanisms acting together.

In the first scenario, there are some examples of molecular players described in the fruit fly that are expressed at tricellular junctions and could work as ‘topological sensors’. In plants, some level of coordination (and neighbour ‘counting’) could be achieved through plasmodesmata.

We favoured the second scenario and believe that our work calls for explanations that reconcile and integrate cell shape and topology into account. Regarding the molecular basis of this, I think it is still an open question.

RC One idea we did come up with we termed the ‘tent model’ of cell division. The number of triple junctions formed on the cell membrane, where it joins with other cells, is equal to the number of neighbours for that cell. These junctions have been shown to exert a tension on the cell membrane. If a cell can somehow measure this tension locally, possibly by use of mechanosensitve ion channels, it could place the mitotic spindle as to divide these neighbours in half.

Ross and Yara, when doing the research, did you have any particular result or eureka moment that has stuck with you?

YSC I was very surprised to know that the complex shape of the PC cells has no influence in the topological profile, as the signature is very similar at early and late stages. The other surprising result for me was that a very simple rule could recapitulate very well the topological pattern we observe in the data.

RC I remember when we were investigating division rules and looking at the resulting neighbour distributions we couldn’t find one that matched our data very well. I was in a meeting with Stan and we ended the meeting by saying ‘I wonder what happens if we just split the neighbourhood in half?’. I added the rule to our model and half an hour later checked the results and the distributions matched almost exactly! I recall going back to Stan’s office and both getting quite excited!

And what about on the flipside: any moments of frustration or despair?

YSC It was very challenging to acquire time-lapse data of a slowly growing tissue. I had all the support from the Coen’s lab, especially from Samantha Fox.  But, I still tried many times and make all possible mistakes before acquiring good data sets.

RC As above! We got to the point where none of the division rules we tried were matching our data, as a last attempt we tried the equal split rule, and it worked!

What are you career plans following this work?

YSC In my postdoctoral work, I am looking at a related aspect of topology: the case when cells exchange neighbours in a polarised manner.

RC I’m currently in another post-doc position at the Sainsbury Laboratory, Cambridge University. Here I’m doing research into modelling the mechanics of morphogenesis in the group of Prof. Henrik Jönsson. I hope to be applying for fellowships next year and to become a bit more independent in the future.

Verônica and Stan, where do you think this work will take your labs?

AM & VG Other groups, like the one of George Bassel, have found interesting topological hierarchies and control for other plant tissues. We think that the community is now realising that these topologies, which are all unique and can only be explained as being tightly regulated on the topological level, points to some form of functionality. As we are also working with nutrient uptake in roots, we wish to explore how topological connectedness of cells could be related to the transport dynamics. In the light of the leaf, we hope to continue to explore how changes in mitosis could distort these topological patterns, and possibly, how this might influence other patterning, communication, and developmental aspects.

Finally, what do you like to do when you are not in the lab?

AM & VG We both love hiking through forests, mountains, marsh lands etc. We now enjoy these nature walks with our two small children, carrying the smallest one, who is one-year-old, on our back, while our 4-year-old jumps ahead like a mountain goat. They are teaching us to “re-see” the world around us, as well as our human condition – with a renewed wonder and a fresh set of questions –  from a whole new perspective.

YSC I like cooking (especially Mexican food) and enjoy walking in the countryside.

RC I really enjoy getting out in to the countryside on my bike, painting and drawing, and live music!

Thank you!

Ross Carter, Yara E. Sánchez-Corrales, Matthew Hartley, Verônica A. Grieneisen, Athanasius F. M. Marée. 2017. Pavement cells and the topology puzzle. Development. Volume 144, Issue 23, p4386-4397.

This is #33 in our interview series. Browse the archive here. 

(No Ratings Yet)

Loading...